Happy Clown Carnival Company is scheduled to appear in a city on a given date. The carnival has to set up equipment for its show, but it can cancel the show prior to setting up its equipment. The profits that will be obtained depend heavily upon the weather. In particular, if the Carnival sets up and the weather is rainy, the carnival averages a $15.000 loss: if it is not rainy, the carnival averages a $5000 profit. A cancellation results in a loss of $1.000. The Weather Bureau has compiled a prior probability distribution for the weather on this day of the year that shows a 90% chance it will not be rainy, and a 10% chance its going to be rainy.

a. Construct a payoff table for the prior analysis. Then, using the maximum expected payoff criterion, determine Happy Clown's best action (SETUP or CANCEL) and the associated expected payoff.

b. Determine the expected value of perfect information (EVPI) for this situation.

Consider the decision problem with the following additional option. Suppose, for an additional $400 cost the carnival can postpone its setup decision until the day before the scheduled performance. At that time, the carnival can obtain the local weather report. The Weather Bureau has compiled data based upon its predictions in the past, as shown in the conditional forecast probability table below.

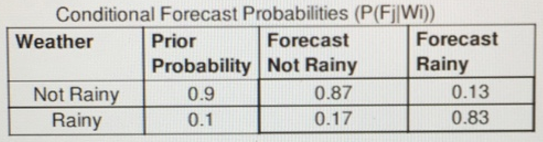
Hence it the weather is Rainy, the forecast is correct with probability 0.83, whereas is correct with probability 0.83, whereas it the wheather is Not Rainy, the forecast is correct with probability 0.87.

The joint probability table for this situation is readily seen to be as follows:

And the resulting posterior probability distirbutions are as follows:

c. Construct the decision tree for the entire decision (including also the opportunity of waiting for the weather lorecast). By backward induction, determine Happy Clown?s optimal decision rule, Clearly state the decision rule obtained and Happy Clown?s maximum expected payoff. For that rule, EMV*.

Conditional Forecast Probabilities (P(Fj|Wi)) Prior Forecast Probability Not Rainy 0.9 0.87 0.1 0.17 Weather Not Rainy Rainy Forecast Rainy 0.13 0.83 NR R F.NR 0.783 0.017 0.8 F.R 0.117 0.083 0.2 0.9 0.1 NR R F.NR 0.97875 0.02125 1 F.R 0.585 0.415 1