Let G be a finite group.

(i) Prove that elements in the same conjugacy class have conjugate centralizers.

(ii) If c ₁ ,?. , c _r are the orders of the centralizers of elements from the distinct conjugacy classes prove that

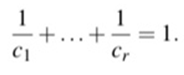
1 ci +...+ 1 Cr = 1.