Tank-draining with a siphon?M. Fig. shows a tank of horizontal cross-sectional area A that is supplied with a steady volumetric flow rate Q of liquid, and that is simultaneously being drained through a siphon of cross-sectional area a, whose discharge is at the same level as the base of the tank. Frictional dissipation in the siphon may be neglected.

Fig. Siphon for draining tank.

(a) Assuming that pipe friction is negligible, prove that the steady-state level in the tank is given by:

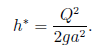
(b) if the incoming flow rate of liquid is now suddenly increased to 2Q, prove that the time taken for the depth of liquid to rise to 2tr (shown by the uppermost dashed line) is given by the following expression, in which you are expected to compute the value of the coefficient a:

You should need one of the integrals given in Appendix A. Start by performing a transient mass balance on the tank when the depth of liquid is h, between h*and 2h*. Comment on the fact that the higher the follow rate, the longer the time it will take!

Transcribed Image Text:

2h* h(t) h* Q Tank Siphon Discharge h* Q² 2ga² 2h* h(t) h* Q Tank Siphon Discharge h* Q² 2ga²

Answer rating: 100% (QA)

The inlet flow rate to the tank is Q and the initial height of the liquid surface of the tank is The ... View the full answer