Question: The surface S' is a hemispherical surface of radius A created by the circular loop C. The hemisphere S' lies entirely in the volume of
The surface S' is a hemispherical surface of radius A created by the circular loop C. The hemisphere S' lies entirely in the volume of negative z.
(a) Write down the vector in Cartesian coordinate of a tiny portion of surface on S'which has an area da near the location (-A, 0, 0)?
(b) Calculate the surface integral over this open surface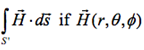 
is a spherical coordinate function of 
. In this question, please use the convention of ? to be the polar angle (from 0 to ?), while ? to be the azimuthal angle (from ? to 2?).
S' -ds if (r,0,0) = / (/r-rcos 00)
Step by Step Solution
3.38 Rating (145 Votes )
There are 3 Steps involved in it
To solve this problem lets approach it step by step a Vector of a Tiny Portion of Surface on S The hemispherical surface S is defined by a radius A an... View full answer
Get step-by-step solutions from verified subject matter experts