Question: 0 Question 23 B 0/1 pt '0 3 8 99 (9 Details 14% of all college students volunteer their time. Is the percentage of college




![: I? v Select an answer v C] (please enter a decimal)](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666db68592089_181666db6856bd18.jpg)
![H1 : ? v Select an answer v [:] (Please enter a](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666db686067eb_181666db685cd242.jpg)
![decimal) c. The test statistic = C] (please show your answer to](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666db6868d83c_182666db6866b07e.jpg)
![3 decimal places.) d. The p-value = C] (Please show your answer](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666db686f0499_182666db686cf1b7.jpg)



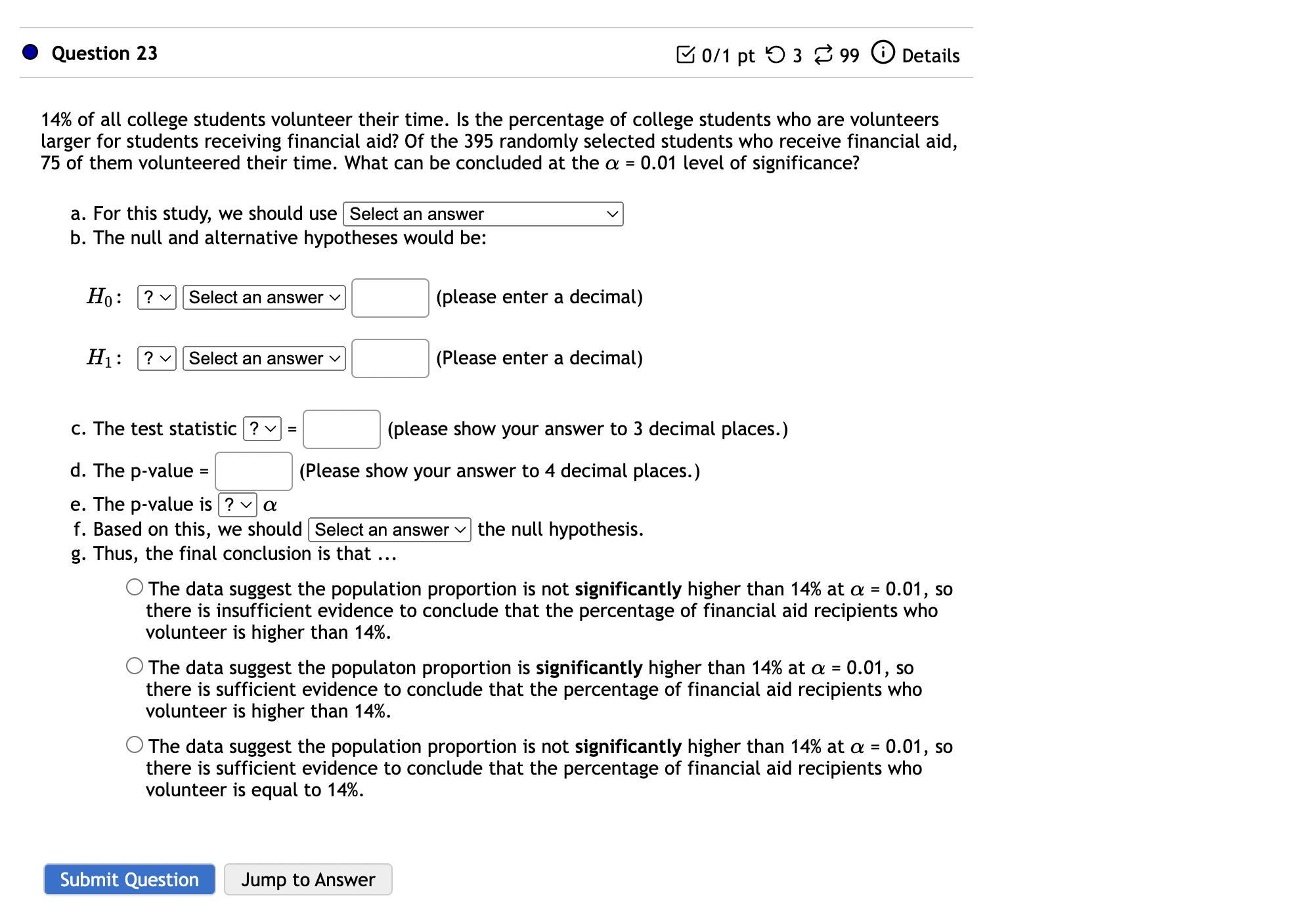



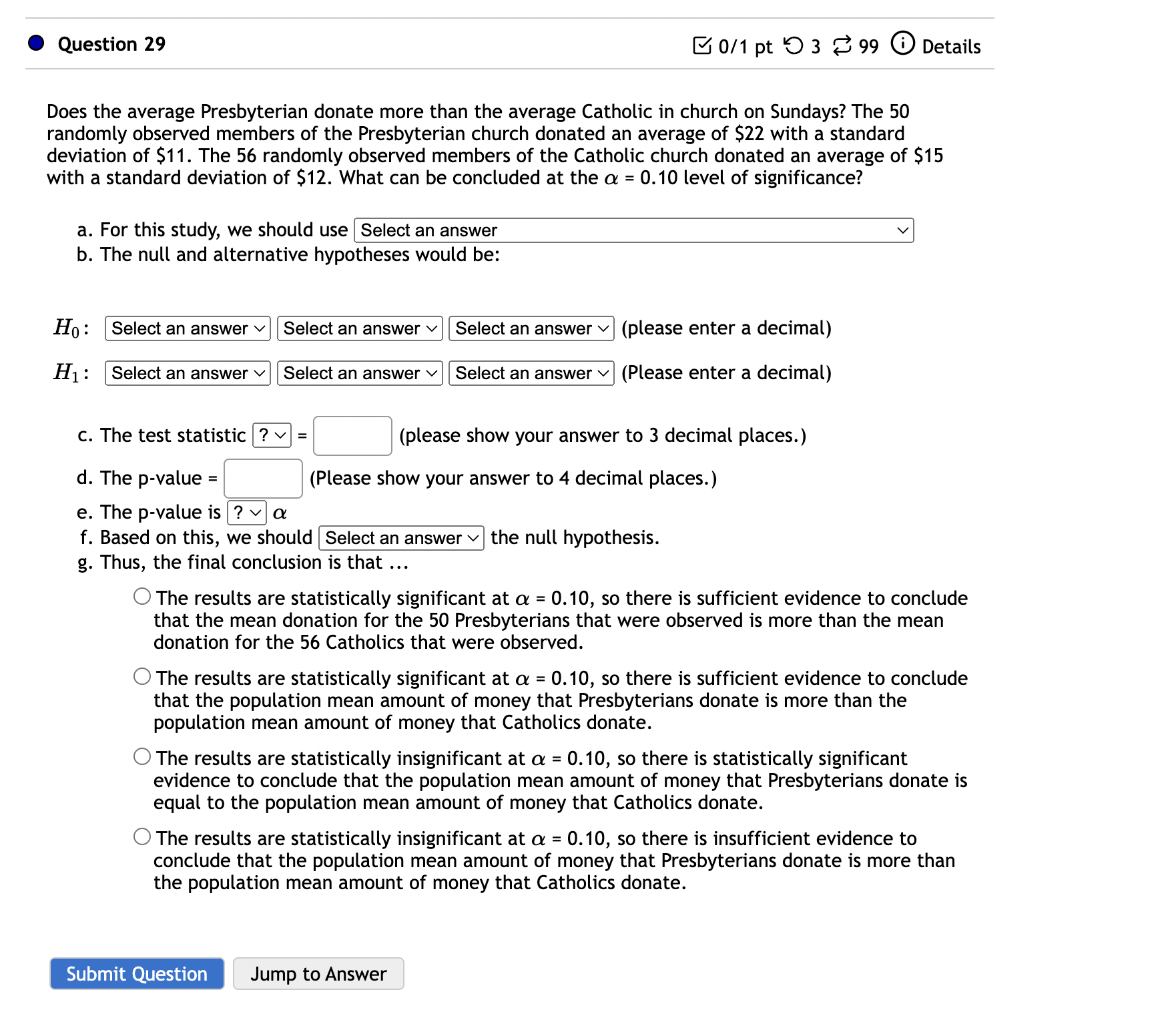
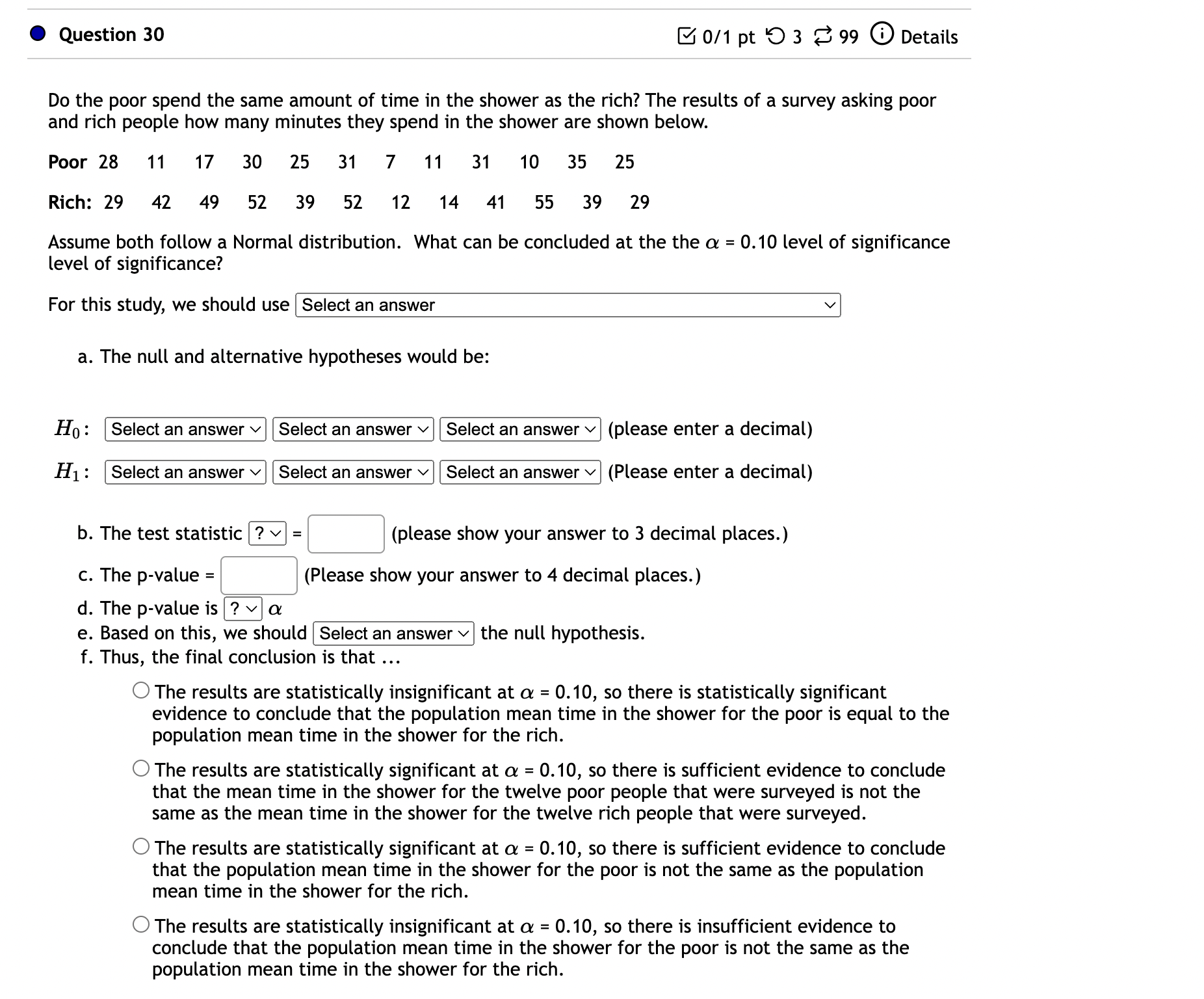


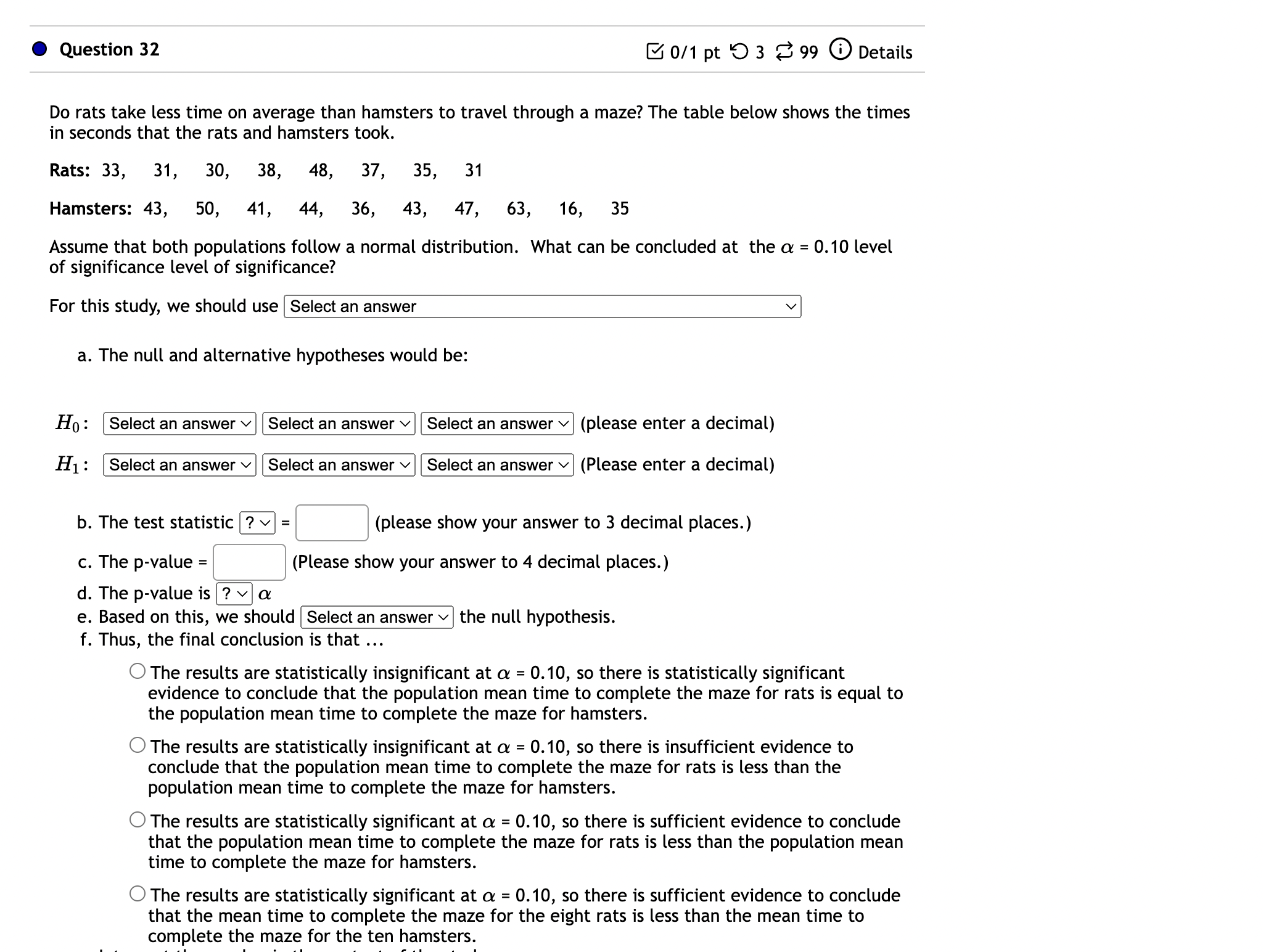




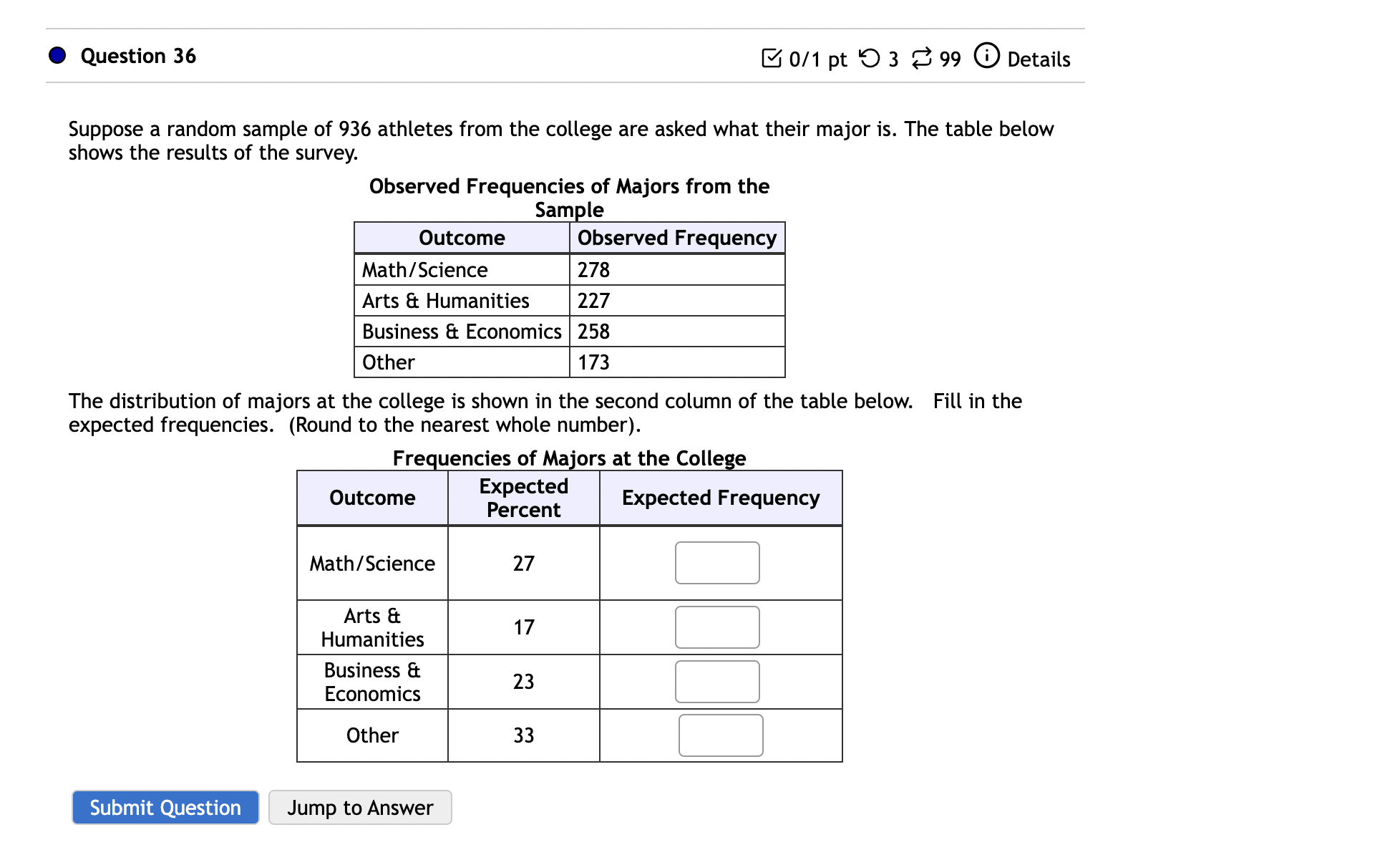

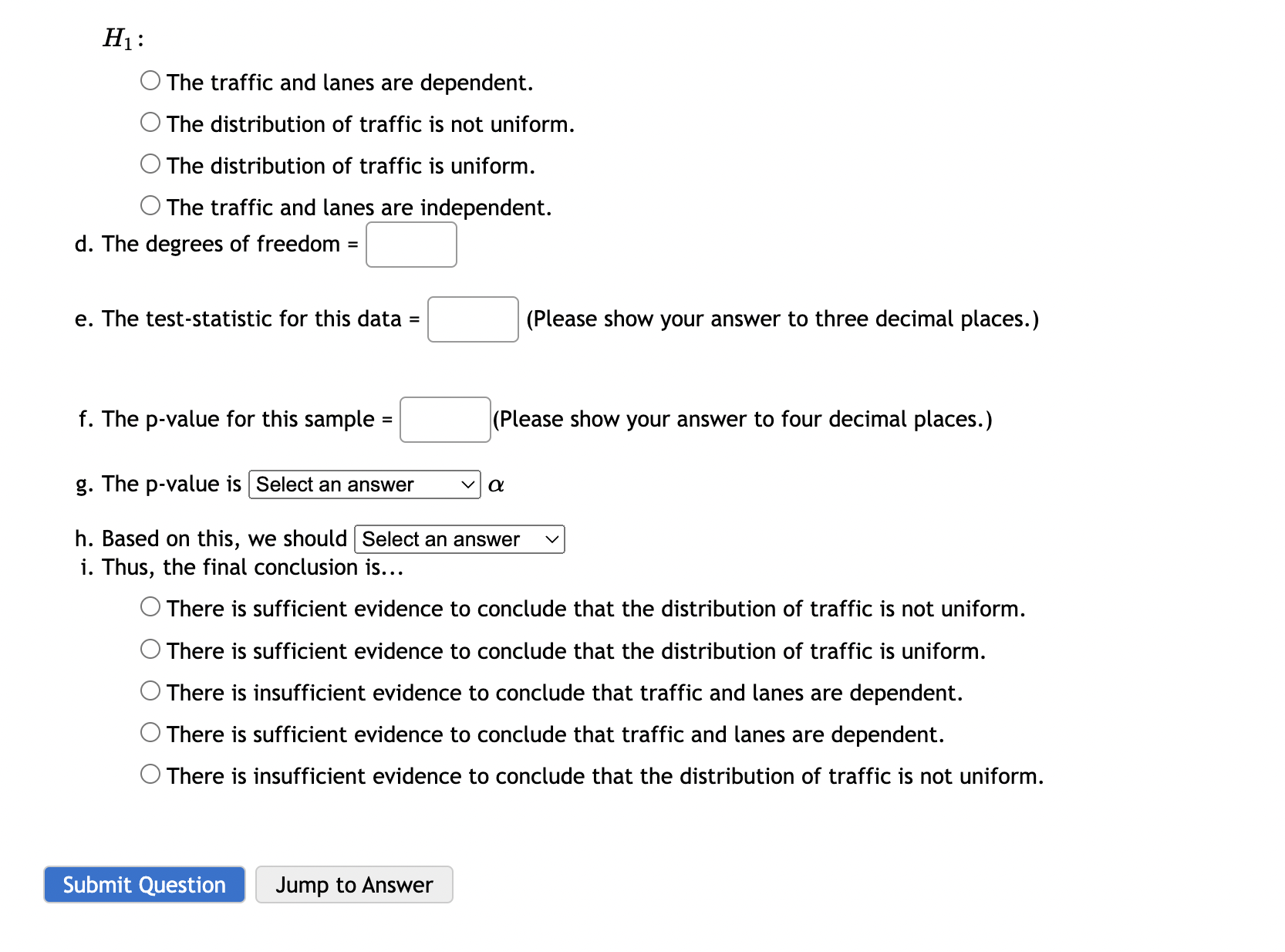
0 Question 23 B 0/1 pt '0 3 8 99 (9 Details 14% of all college students volunteer their time. Is the percentage of college students who are volunteers larger for students receiving financial aid? Of the 395 randomly selected students who receive financial aid, 75 of them volunteered their time. What can be concluded at the a = 0.01 level of significance? a. For this study, we should use Select an answer v b. The null and alternative hypotheses would be: Hg : I? v Select an answer v C] (please enter a decimal) H1 : ? v Select an answer v [:] (Please enter a decimal) c. The test statistic = C] (please show your answer to 3 decimal places.) d. The p-value = C] (Please show your answer to 4 decimal places.) e. The p-value is a f. Based on this, we should the null hypothesis. g. Thus, the final conclusion is that O The data suggest the population proportion is not significantly higher than 14% at a = 0.01, so there is insufficient evidence to conclude that the percentage of financial aid recipients who volunteer is higher than 14%. O The data suggest the populaton proportion is significantly higher than 14% at a = 0.01, so there is sufficient evidence to conclude that the percentage of financial aid recipients who volunteer is higher than 14%. O The data suggest the population proportion is not significantly higher than 14% at a = 0.01, so there is sufficient evidence to conclude that the percentage of financial aid recipients who volunteer is equal to 14%. Submit Question Jump to Answer Is the average time to complete an obstacle course different when a patch is placed over the right eye than when a patch is placed over the left eye? Thirteen randomly selected volunteers first completed an obstacle course with a patch over one eye and then completed an equally difficult obstacle course with a patch over the other eye. The completion times are shown below. "Left" means the patch was placed over the left eye and "Right" means the patch was placed over the right eye. Time to Com - lete the Course umuummuuu Assume a Normal distribution. What can be concluded at the the a = 0.05 level of significance level of significance? For this study. we should use a. The null and alternative hypotheses would be: H0 : Select an answer v Select an answer v Select an answer v (please enter a decimal) H1: Select an answer v Select an answer v Select an answer v (Please enter a decimal) b. The test statistic = [3 (please show your answer to 3 decimal places.) c. The p-value = [:] (Please show your answer to 4 decimal places.) d. The p-value is a e. Based on this, we should the null hypothesis. f. Thus, the final conclusion is that O The results are statistically insignificant at a = 0.05, so there is statistically significant evidence to conclude that the population mean time to complete the obstacle course with a patch over the right eye is equal to the population mean time to complete the obstacle course with a patch over the left eye. 0 The results are statistically significant at a = 0.05, so there is sufficient evidence to conclude that the eight volunteers that were completed the course in the same amount of time on average with the patch over the right eye compared to the left eye. 0 The results are statistically significant at a = 0.05, so there is sufficient evidence to conclude that the population mean time to complete the obstacle course with a patch over the right eye is not the same as the population mean time to complete the obstacle course with a patch over the left eye. 0 The results are statistically insignificant at a = 0.05, so there is insufficient evidence to conclude that the population mean time to complete the obstacle course with a patch over the right eye is not the same as the population mean time to complete the obstacle course with a 0 Question 28 B 0/1 pt '0 3 8 99 (D Details ls memory ability before a meal better than after a meal? Ten people were given memory tests before their meal and then again after their meal. The data is shown below. A higher score indicates a better memory ability. Score on the Memo Test Assume a Normal distribution. What can be concluded at the the a = 0.10 level of significance? For this study, we should use Select an answer v a. The null and alternative hypotheses would be: H0: Select an answer v Select an answer v Select an answer v (please enter a decimal) H1: Select an answer v Select an answer v Select an answer v (Please enter a decimal) b. The test statistic = 1:] (please show your answer to 3 decimal places.) c. The p-value = C] (Please show your answer to 4 decimal places.) d. The p-value is a e. Based on this, we should the null hypothesis. f. Thus, the final conclusion is that O The results are statistically insignificant at a = 0.10, so there is insufficient evidence to conclude that the population mean memory score before a meal is higher than the population mean memory score after a meal. 0 The results are statistically significant at a = 0.10, so there is sufficient evidence to conclude that the population mean memory score before a meal is higher than the population mean memory score after a meal 0 The results are statisticallyinsignificant at a = 0.10, so there is statistically significant evidence to conclude that the population mean memory score before a meal is equal to the population mean memory score after a meal. L) The results are statistically significant at a = 0.10, so there is sufficient evidence to conclude that the population mean memory score before a meal is higher than the population mean memory score after a meal 0 The results are statistically insignificant at a = 0.10, so there is statistically significant evidence to conclude that the population mean memory score before a meal is equal to the population mean memory score after a meal. 0 The results are statistically significant at a = 0.10, so there is sufficient evidence to conclude that the ten memory scores from the memory tests that were taken before a meal are higher on average than the ten memory scores from the memory tests that were taken after a meal. g. Interpret the p-value in the context of the study. 0 There is a 60.37% chance of a Type I error. 0 There is a 60.37% chance that the mean memory score for the 10 people who took the test before a meal is at least 0.4 points higher than the mean memory score for the 10 people who took the test after a meal. 0 If the sample mean memory score for the 10 people who took the test before a meal is the same as the sample mean memory score for the 10 people who took the test after a meal and if another 10 people are given a memory test before and after a meal then there would be a 60.37% chance of concluding that the mean memory score for the 10 people who took the test before a meal is at least 0.4 points higher than the mean memory score for the 10 people who took the test after a meal. 0 If the population mean memory score before a meal is the same as the population mean memory score after a meal and if another 10 people are given a memory test before and after a meal then there would be a 60.37% chance that the mean memory score for the 10 people who took the test before a meal would be at least 0.4 points higher than the mean memory score for the 10 people who took the test after a meal. h. Interpret the level of significance in the context of the study. 0 There is a 10% chance that your memory is so bad that you have already forgotten what this chapter is about. 0 There is a 10% chance that the population mean memory score is the same before and after a meal. 0 If the population mean memory score before a meal is the same as the population mean memory score after a meal and if another 10 people are given a memory test before and after a meal, then there would be a 10% chance that we would end up falsely concuding that the population mean memory score before a meal is higher than the population mean memory score after a meal 0 If the population mean memory score before a meal is the same as the population mean memory score after a meal and if another 10 people are given a memory test before and after a meal, then there would be a 10% chance that we would end up falsely concuding that the sample mean memory scores before and after a meal for these 10 people who were part of the study differ from each other. 0 Question 29 Ea" 0/1 pt '0 3 8 99 G Details Does the average Presbyterian donate more than the average Catholic in church on Sundays? The 50 randomly observed members of the Presbyterian church donated an average of $22 with a standard deviation of $11. The 56 randomly observed members of the Catholic church donated an average of $15 with a standard deviation of $12. What can be concluded at the a = 0.10 level of significance? a. For this study, we should use Select an answer v b. The null and alternative hypotheses would be: H0 : Select an answer v Select an answer v Select an answer v (please enter a decimal) H1 : Select an answer v Select an answer v Select an answer v (Please enter a decimal) c. The test statistic = [:] (please show your answer to 3 decimal places.) d. The p-value = C] (Please show your answer to 4 decimal places.) e. The p-value is a f. Based on this, we should the null hypothesis. g. Thus, the final conclusion is that O The results are statistically significant at a = 0.10, so there is sufficient evidence to conclude that the mean donation for the 50 Presbyterians that were observed is more than the mean donation for the 56 Catholics that were observed. 0 The results are statistically significant at a = 0.10, so there is sufficient evidence to conclude that the population mean amount of money that Presbyterians donate is more than the population mean amount of money that Catholics donate. O The results are statistically insignificant at a = 0.10, so there is statistically significant evidence to conclude that the population mean amount of money that Presbyterians donate is equal to the population mean amount of money that Catholics donate. 0 The results are statistically insignificant at a = 0.10, so there is insufficient evidence to conclude that the population mean amount of money that Presbyterians donate is more than the population mean amount of money that Catholics donate. Submit Question Jump to Answer 0 Question 30 B 0/1 pt '0 3 8 99 6) Details Do the poor spend the same amount of time in the shower as the rich? The results of a survey asking poor and rich people how many minutes they spend in the shower are shown below. Poor 28 11 17 30 25 31 7 11 31 10 35 25 Rich: 29 42 49 52 39 52 12 14 41 55 39 29 Assume both follow a Normal distribution. What can be concluded at the the a = 0.10 level of significance level of significance? For this study, we should use [ Select an answer \\/I a. The null and alternative hypotheses would be: H0 : Select an answer v Select an answer v Select an answer v (please enter a decimal) H1 : [Select an answer vl [Select an answer v [Select an answer vl (Please enter a decimal) b. The test statistic = [2 (please show your answer to 3 decimal places.) c. The p-value = [:[ (Please show your answer to 4 decimal places.) d. The p-value is ? v a e. Based on this, we should the null hypothesis. f. Thus, the final conclusion is that O The results are statistically insignificant at a = 0.10, so there is statistically significant evidence to conclude that the population mean time in the shower for the poor is equal to the population mean time in the shower for the rich. 0 The results are statistically significant at a = 0.10, so there is sufficient evidence to conclude that the mean time in the shower for the twelve poor people that were surveyed is not the same as the mean time in the shower for the twelve rich people that were surveyed. O The results are statistically significant at a = 0.10, so there is sufficient evidence to conclude that the population mean time in the shower for the poor is not the same as the population mean time in the shower for the rich. 0 The results are statistically insignificant at a = 0.10, so there is insufficient evidence to conclude that the population mean time in the shower for the poor is not the same as the population mean time in the shower for the rich. 0 Question 31 8 0/1 pt '0 3 8 99 G Details Do men take a different amount of time than women to get out of bed in the morning? The 43 men observed averaged 5.7 minutes to get out of bed after the alarm rang. Their standard deviation was 2.8. The 58 women observed averaged 7 minutes and their standard deviation was 1.4 minutes. What can be concluded at the a = 0.05 level of significance? a. For this study, we should use Select an answer v b. The null and alternative hypotheses would be: H0: Select an answer v Select an answer v Select an answer v (please enter a decimal) H1: Select an answer v Select an answer v Select an answer v (Please enter a decimal) c. The test statistic = C] (please show your answer to 3 decimal places.) d. The p-value = [2 (Please show your answer to 4 decimal places.) e. The p-value is a f. Based on this, we should the null hypothesis. g. Thus, the final conclusion is that O The results are statistically insignificant at a = 0.05, so there is insufficient evidence to conclude that the population mean time for men to get out of bed in the morning is different than the population mean time for women to get out of bed in the morning. 0 The results are statistically significant at a = 0.05, so there is sufficient evidence to conclude that the mean time to get out of bed in the morning for the 43 men that were observed is different than the mean time for the 58 women that were observed. 0 The results are statistically insignificant at a = 0.05, so there is statistically significant evidence to conclude that the population mean time for men to get out of bed in the morning is equal to the population mean time for women to get out of bed in the morning. 0 The results are statistically significant at o: = 0.05, so there is sufficient evidence to conclude that the population mean time for men to get out of bed in the morning is different than the population mean time for women to get out of bed in the morning. h. Interpret the p-value in the context of the study. 0 If the sample mean time to get out of bed in the morning for the 43 men is the same as the sample mean time to get out of bed in the morning for the 58 women and if another 43 men and 58 women are observed then there would be a 0.7% chance of concluding that the mean time to get out of bed in the morning for the 43 men differs by at least 1.3 minutes from the mean time to get out of bed in the morning for the 58 women h. Interpr'e'trt'ri'vam'ih't'ii'til'b?'t'e ZEdd'yT' " W\" C) If the sample mean time to get out of bed in the morning for the 43 men is the same as the sample mean time to get out of bed in the morning for the 58 women and if another 43 men and 58 women are observed then there would be a 07% chance of concluding that the mean time to get out of bed in the morning for the 43 men differs by at least 1.3 minutes from the mean time to get out of bed in the morning for the 58 women 0 There is a 0.7% chance that the mean time to get out of bed in the morning for the 43 men differs by at least 1.3 minutes from the mean time to get out of bed in the morning for the 58 women. 0 If the population mean time for men to get out of bed in the morning is the same as the population mean time for women to get out of bed in the morning and if another 43 men and 58 women are observed then there would be a 0.7% chance that the mean time to get out of bed in the morning for the 43 men would differ from the mean time to get out of bed in the morning for the 58 women by at least 1.3 minutes. 0 There is a 0.7% chance of a Type I error. i. Interpret the level of significance in the context of the study. 0 If the population mean time for men to get out of bed in the morning is the same as the population mean time for women to get out of bed in the morning and if another 43 men and 58 women are observed then there would be a 5% chance that we would end up falsely concluding that the population mean time for men to get out of bed in the morning is different than the population mean time for women to get out of bed in the morning 0 There is a 5% chance that there is a difference in the population mean time for men and women to get out of bed in the morning. 0 If the population mean time for men to get out of bed in the morning is the same as the population mean time for women to get out of bed in the morning and if another 43 men and 58 women are observed then there would be a 5% chance that we would end up falsely concluding that the sample mean time for these 43 men and 58 women to get out of bed in the morning differ from each other. 0 There is a 5% chance you will take so long to get out of bed in the morning that you will miss the deadline to complete this assignment. 0 Question 32 B 011 pt '0 3 8 99 (D Details Do rats take less time on average than hamsters to travel through a maze? The table below shows the times in seconds that the rats and hamsters took. Rats: 33, 31, 30, 38, Hamsters: 43, 50, 41, 48, 37, 35, 44, 36, 43, 31 47, 63, 16, 35 Assume that both populations follow a normal distribution. What can be concluded at the a = 0.10 level of significance level of significance? For this study, we should use Select an answer VI a. The null and alternative hypotheses would be: H0: Select an answer v Select an answer v [Select an answer v| (please enter a decimal) H1: Select an answer v Select an answer v [Select an answer v] (Please enter a decimal) b. The test statistic = C] (please show your answer to 3 decimal places.) c. The p-value = [:] (Please show your answer to 4 decimal places.) d. The p-value is ? v a e. Based on this, we should Select an answer v f. Thus, the final conclusion is that the null hypothesis. 0 The results are statistically insignificant at a = 0.10, so there is statistically significant evidence to conclude that the population mean time to complete the maze for rats is equal to the population mean time to complete the maze for hamsters. O The results are statistically insignificant at a = 0.10, so there is insufficient evidence to conclude that the population mean time to complete the maze for rats is less than the population mean time to complete the maze for hamsters. O The results are statistically significant at a = 0.10, so there is sufficient evidence to conclude that the population mean time to complete the maze for rats is less than the population mean time to complete the maze for hamsters. O The results are statistically significant at a = 0.10, so there is sufficient evidence to conclude that the mean time to complete the maze for the eight rats is less than the mean time to complete the maze for the ten hamsters. lUII I'JICLI: LI I: IIIuLC IUI LI II: LCII IlaIIIJLCI :I. g. Interpret the p-value in the context of the study. 0 If the sample mean time to complete the maze for the 8 rats is the same as the sample mean time to complete the maze for the 10 hamsters and if another 8 rats and 10 hamsters are observed then there would be a 8.02% chance of concluding that the mean time to complete the maze for the 8 rats is at least 6.4 seconds less than the mean time to complete the maze for the 10 hamsters. 0 If the population mean time to complete the maze for rats is the same as the population mean time to complete the maze for hamsters and if another 8 rats and 10 hamsters are observed then there would be a 8.02% chance that the mean time to complete the maze for the 8 rats would be at least 6.4 seconds less than the mean time to complete the maze for the 10 hamsters. 0 There is a 8.02% chance that the mean time to complete the maze for the 8 rats is at least 6.4 seconds less than the mean time to complete the maze for the 10 hamsters. 0 There is a 8.02% chance of a Type I error. h. Interpret the level of significance in the context of the study. 0 If the population mean time to complete the maze for rats is the same as the population mean time to complete the maze for hamsters and if another 8 rats and 10 hamsters are observed then there would be a 10% chance that we would end up falsely concluding that the population mean time to complete the maze for rats is less than the population mean time to complete the maze for hamsters 0 There is a 10% chance that the population mean time to complete the maze for rats and hamsters is the same. 0 If the population mean time to complete the maze for rats is the same as the population mean time to complete the maze for hamsters and if another 8 rats and 10 hamsters are observed, then there would be a 10% chance that we would end up falsely concluding that the sample mean time to complete the maze for these 8 rats and 10 hamsters differ from each other. 0 There is a 10% chance that the rat will eat the hamster. 0 Question 33 E\" 0/1 pt '0 3 Z 99 (D Details Are couples that live together before they get married less likely to end up divorced within five years of marriage compared to couples that live apart before they get married? 208 of the 629 couples from the study who lived together before they got married were divorced within five years of marriage. 169 of the 498 couples from the study who lived apart before they got married were divorced within five years of marriage. What can be concluded at the a = 0.10 level of significance? For this study, we should use [Select an answer v| a. The null and alternative hypotheses would be: H 0: [Select an answer v I Select an answer VI Select an answer v H1: [Select an answer v | Select an answer V| Select an answer v b. The test statistic = C] (please show your answer to 3 decimal places.) c. The p-value = [:[ (Please show your answer to 4 decimal places.) d. The p-value is ? v o: e. Based on this, we should the null hypothesis. f. Thus, the final conclusion is that O The results are statistically significant at a = 0.10, so there is sufficient evidence to conclude that the percent of the 629 couples that lived together before they got married who ended up divorced within five years of marriage is smaller than the percent of the 498 couples that lived apart before they got married who ended up divorced within five years of marriage. 0 The results are statisticallyinsignificant at a = 0.10, so there is insufficient evidence to conclude the percent of all couples that live together before they get married who end up divorced within five years of marriage is smaller than the percent of all couples that live apart before they get married who end up divorced within five years of marriage. 0 The results are statistically insignificant at a = 0.10, so there is statistically significant evidence to conclude that the divorce rate for all couples that live together before they get married is equal to the divorce rate for all couples that live apart before they get married. 0 The results are statistically significant at a = 0.10, so there is sufficient evidence to conclude that the percent of all couples that live together before they get married who end up divorced within five years of marriage is smaller than the percent of all couples that live apart before they get married who end up divorced within five years of marriage. 0 Question 34 E 0/1 pt '0 3 23 99 G Details Are job applicants with easy to pronounce last names more likely to get called for an interview than applicants with difficult to pronounce last names. 624 job applications were sent out with last names that are easy to pronounce and 821 identical job applications were sent out with names that were difficult to pronounce. 392 of the "applicants" with easy to pronounce names were called for an interview while 489 of the "applicants" with difficult to pronounce names were called for an interview. What can be concluded at the 0.10 level of significance? For this study, we should use I Select an answer vI a. The null and alternative hypotheses would be: H0 : Select an answer v Select an answer v Select an answer v (please enter a decimal) H1: Select an answer v Select an answer v Select an answer v (Please enter a decimal) b. The test statistic ? v = C] (please show your answer to 3 decimal places.) c. The p-value = [3 (Please show your answer to 4 decimal places.) d. The p-value is a e. Based on this, we should Select an answer v the null hypothesis. 1'. Thus, the final conclusion is that O The results are statistically insignificant at a = 0.10, so we can conclude that the population proportion of applicants with easy to pronounce names who get called for an interview is equal to the population proportion of applicants with difficult to pronounce names who get called for an interview. 0 The results are statistically insignificant at a = 0.10, so there is insufficient evidence to conclude that applicants with easy to pronounce last names are more likely to get called for an interview compared to applicants with difficult to pronounce last names. 0 The results are statistically significant at a = 0.10, so there is sufficient evidence to conclude that the proportion of the 624 applicants with easy to pronounce names who got called for an interview is greater than the proportion of the 821 applicants with difficult to pronounce names who got called for an interview. 0 The results are statistically significant at a = 0.10, so there is sufficient evidence to conclude that among all possible applicants, people with easy to pronounce last names are more likely to get called for an interview compared to people with difficult to pronounce last names. g. Interpretithe p-value in the context of the study. 7 0 If the sample proportion of applicants with easy to pronounce names who receive a callback is the same as the sample proportion of applicants with difficult to pronounce names who receive a callback and if another another 624 applications with easy to pronounce names and 821 applications with difficult to pronounce names are submitted then there would be a 10.42% chance of concluding that applicants with easy to pronounce names are at least 3.3% more likely to receive a callback than applicants with difficult to pronounce names 0 There is a 10.42% chance that applicants with easy to pronounce names are 3.3% more likely to receive a callback than applicants with difficult to pronounce names. 0 There is a 10.42% chance of a Type I error. Q If the population proportion of callbacks for applicants with easy to pronounce last names is the same as the population proportion of callbacks for applicants with difficult to pronounce last names and if another 624 applications with easy to pronounce names and 821 applications with difficult to pronounce names are submitted then there would be a 10.42% chance that the percent of callbacks for the sample of applicants with easy to pronounce names would be at least 3.3% more than the percent of callbacks for the sample of applicants with difficult to pronounce names. h. Interpret the level of significance in the context of the study. 0 If the population proportion of callbacks for applicants with easy to pronounce last names is the same as the population proportion of callbacks for applicants with difficult to pronounce last names and if another 624 applications with easy to pronounce names and 821 applications with difficult to pronounce names are submitted then there would be a 10% chance that we would end up falsely concuding that the proportion of callbacks for the submitted applications with easy to pronounce last names is greater than the proportion of callbacks for the submitted applications with difficult to pronounce last names. 0 If the population proportion of callbacks for applicants with easy to pronounce last names is the same as the population proportion of callbacks for applicants with difficult to pronounce last names and if another 624 applications with easy to pronounce names and 821 applications with difficult to pronounce names are submitted then there would be a 10% chance that we would end up falsely concuding that the population proportion of callbacks for applicants with easy to pronounce last names is greater than the population proportion of callbacks for applicants with difficult to pronounce last names. 0 There is a 10% chance that the manager's son will get the job, so it is pointless to apply no matter what your last name is. 0 Question 36 B 0/1 pt '0 3 8 99 (D Details Suppose a random sample of 936 athletes from the college are asked what their major is. The table below shows the results of the survey. Observed Frequencies of Majors from the Sam - le m observed Frequency 278 Arts & Humanities 227 Business & Economics 258 Other 173 The distribution of majors at the college is shown in the second column of the table below. Fill in the expected frequencies. (Round to the nearest whole number). Frequencies of Majors at the College Expected Outcome Percent Expected Frequency Math/ Science 27 I: Arts & Humanities 1 7 [:] Business & 23 I: Economics Other 33 C] Submit Question Jump to Answer 0 Question 37 E 0/1 pt '0 3 8 99 6) Detail: You want to see if it makes a difference which lane to be in when there is traffic. You randomly observe 200 cars as they pass by on the four lane freeway. The results are displayed in the table below. Use a level of significance of a = 0.10. a. Complete the rest of the table by filling in the expected frequencies: Fre-uenc of Cars in Each Lane m Expected Frequency \"E- -_E- \"E- b. What is the correct statistical test to use? Select an answer v c. What are the null and alternative hypotheses? H0 1 O The traffic and lanes are independent. 0 The traffic and lanes are dependent. O The distribution of traffic is not uniform. O The distribution of traffic is uniform. O The traffic and lanes are dependent. O The distribution of traffic is not uniform. O The distribution of traffic is uniform. O The traffic and lanes are independent. I\\ O The traffic and lanes are dependent. O The distribution of traffic is not uniform. O The distribution of traffic is uniform. O The traffic and lanes are independent. d. The degrees of freedom = C] e. The test-statistic for this data = C] (Please show your answer to three decimal places.) f. The p-value for this sample = C(Please show your answer to four decimal places.) 9- The P-Value is C! h. Based on this, we should i. Thus, the final conclusion is... 0 There is sufficient evidence to conclude that the distribution of traffic is not uniform. 0 There is sufficient evidence to conclude that the distribution of traffic is uniform. 0 There is insufficient evidence to conclude that traffic and lanes are dependent. 0 There is sufficient evidence to conclude that traffic and lanes are dependent. 0 There is insufficient evidence to conclude that the distribution of traffic is not uniform. Submit Question Jump to
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


