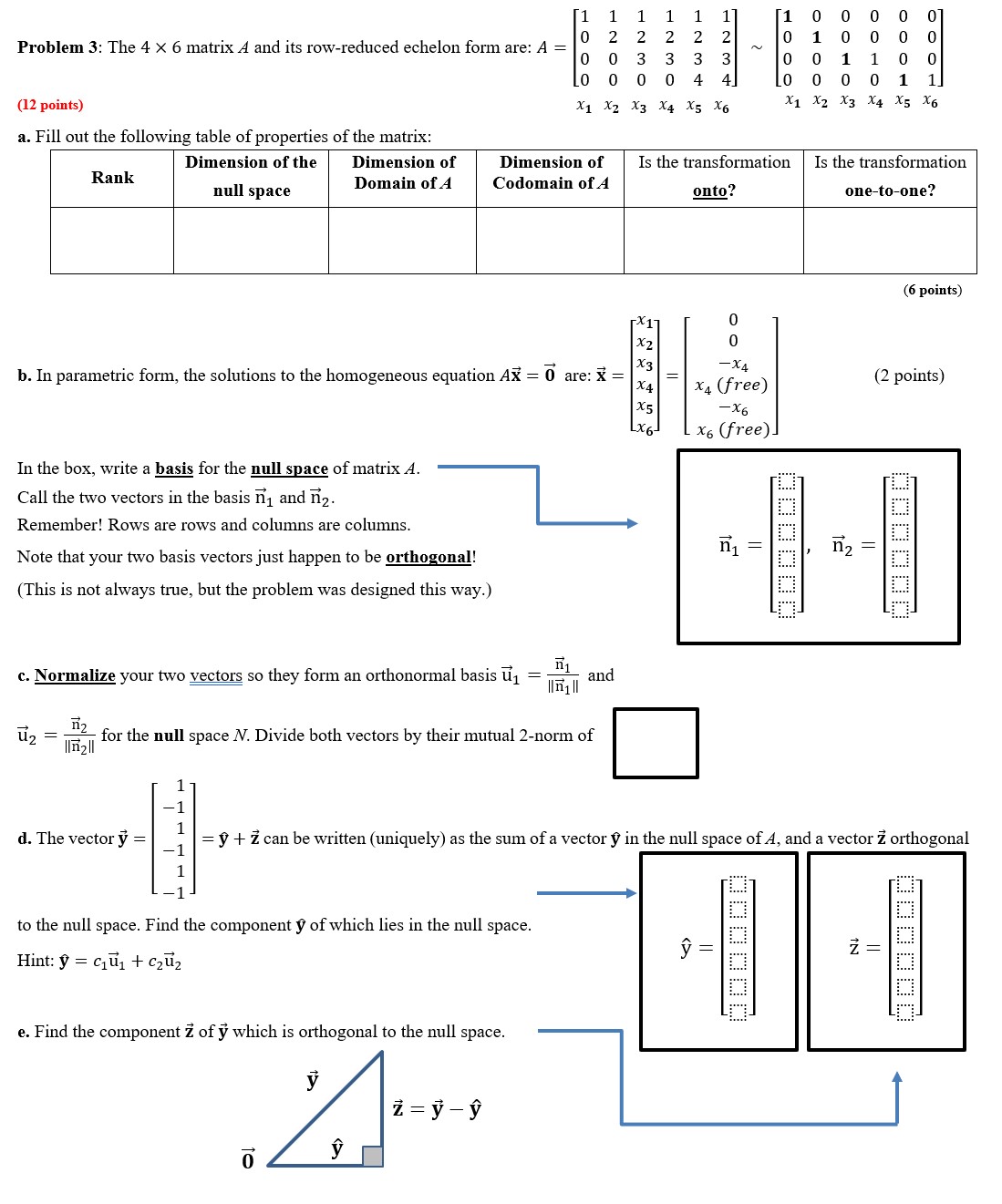
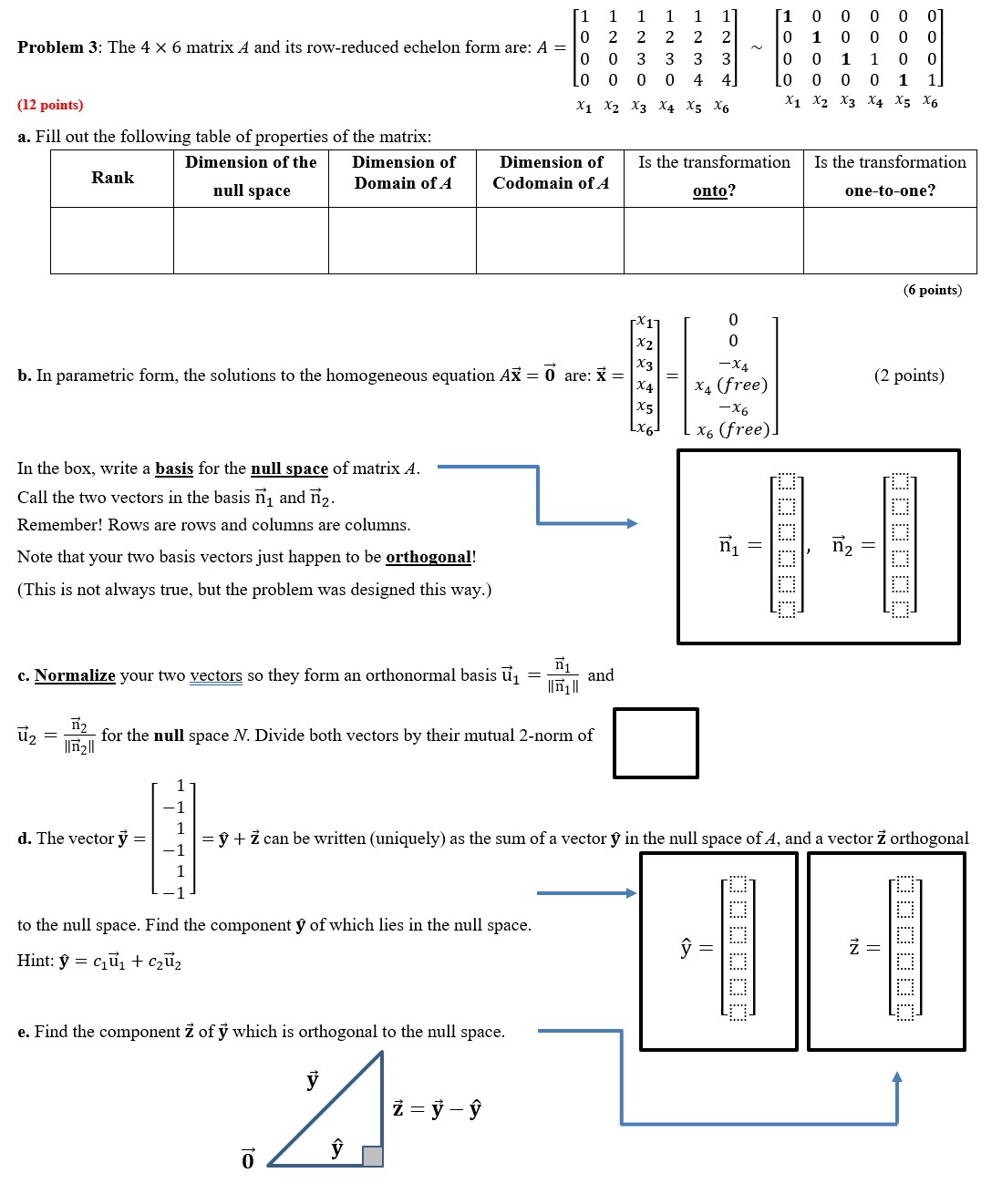
1 1 1 1 1 1 1 0 O 0 0 0 Problem 3: The 4- X 6 matrixA and its row-reduced echelon form are: A = g 3 g g g g N 3 3 2 [1) 3 g 0 0 0 0 4 4 0 0 0 O 1 1 (12 points) x1 x2 x3 x4 x5 x5 3'1 x2 x3 3'! J\"5 3'6 a. Fill out the following table of properties of the matrix: Ra k Dimension of the Dimension of Dimension of Is the transformation Is the transformation n a I null space Domaln OfA Codomam "IA onto? onetoone? (6 points) X1 0 X2 0 . . . ) _' ) X3 _x4 . b. 1n parametric form, the solutions to the homogeneous equation Ax = 0 are: x = x4 = x4 (free) (2 pomts) x5 6 In the box, write a basis for the null space of matrix A. Call the two vectors in the basis 31 and g. Remember! Rows are rows and columns are columns. Note that your two basis vectors just happen to be orthogonal! (This is not always true, but the problem was designed this way.) _, "1 c. Normalize your two vectors so they form an orthonormal basis E} = \"if H and 1 g = llf'Iile for the null space N. Divide both vectors by their mutual 2-norrn of 2 1 1 d. The vector 37 = _: = y + 2' can be written (uniquely) as the sum of a vector 3? in the null space of A, and a vector i orthogonal 1 to the null space. Find the component 9 of which lies in the null space. Hint: ? = 6131 + 9211} e. Find the component 2' of f! which is orthogonal to the null space. 3? i=i 6