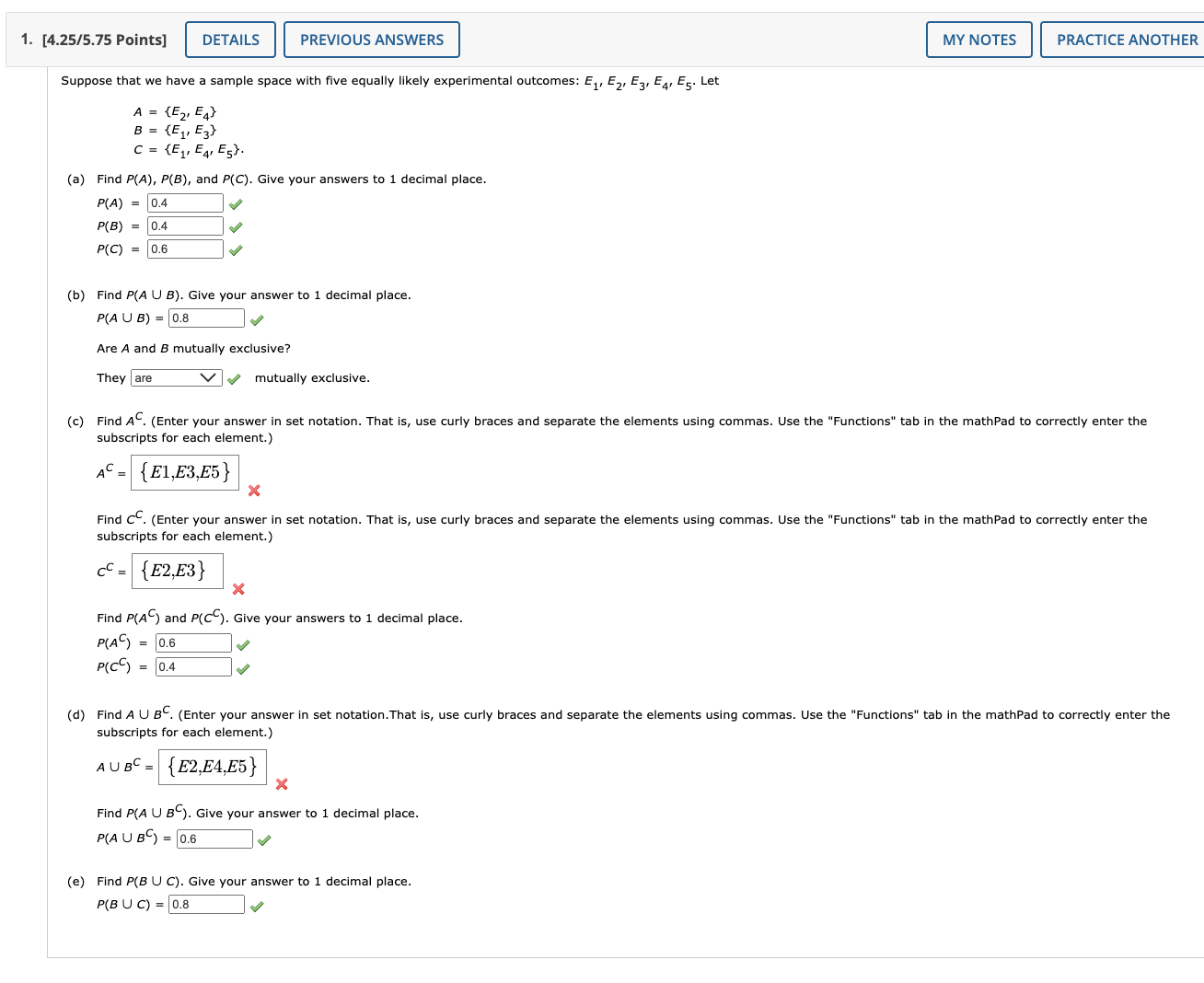
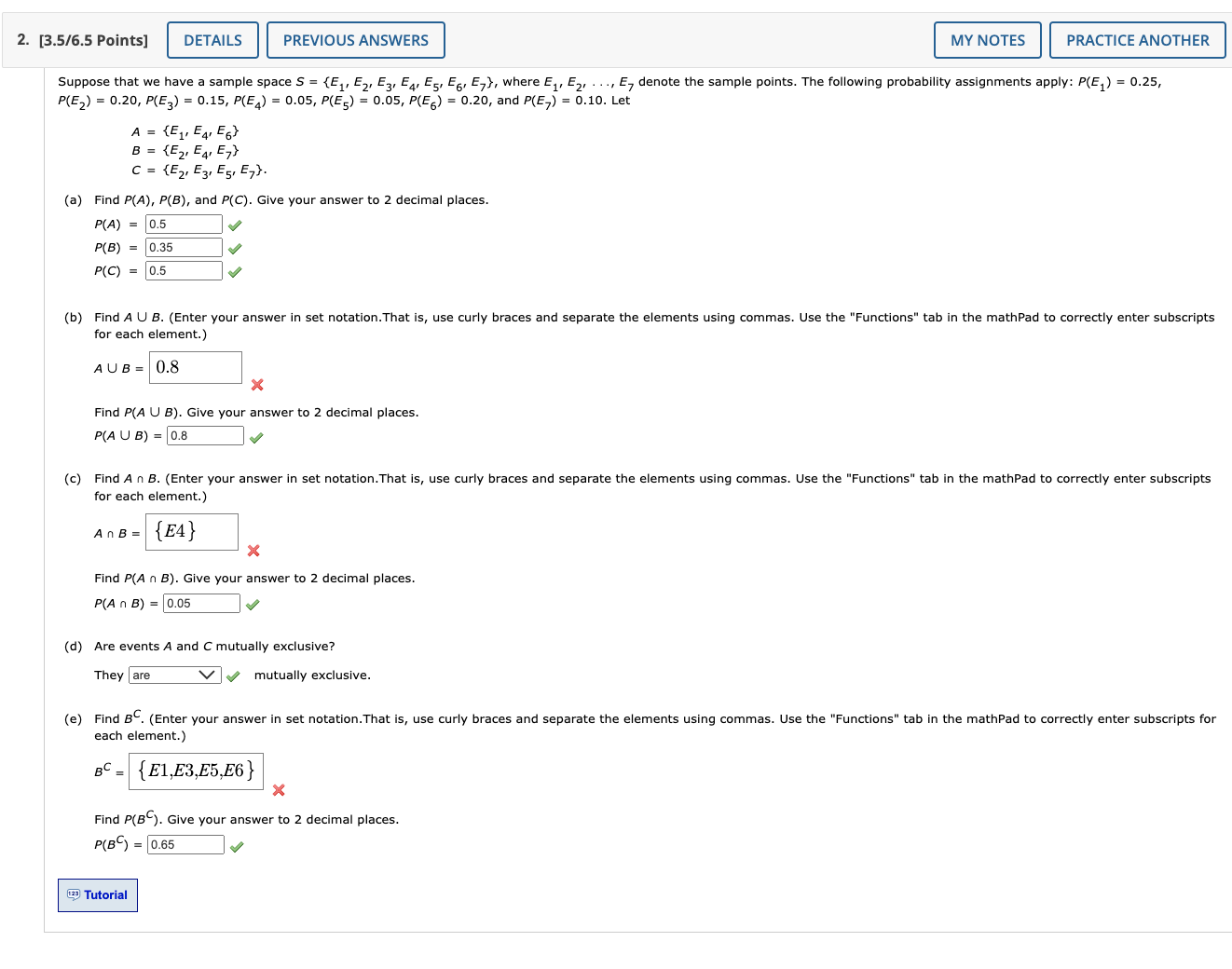
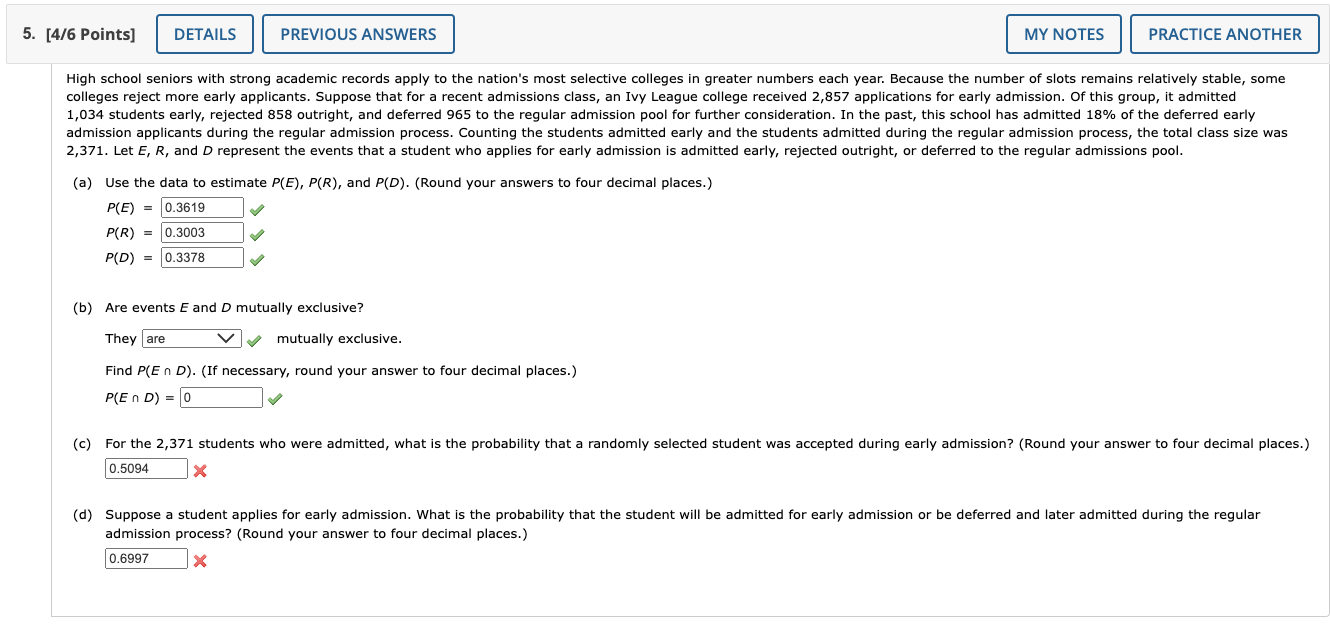
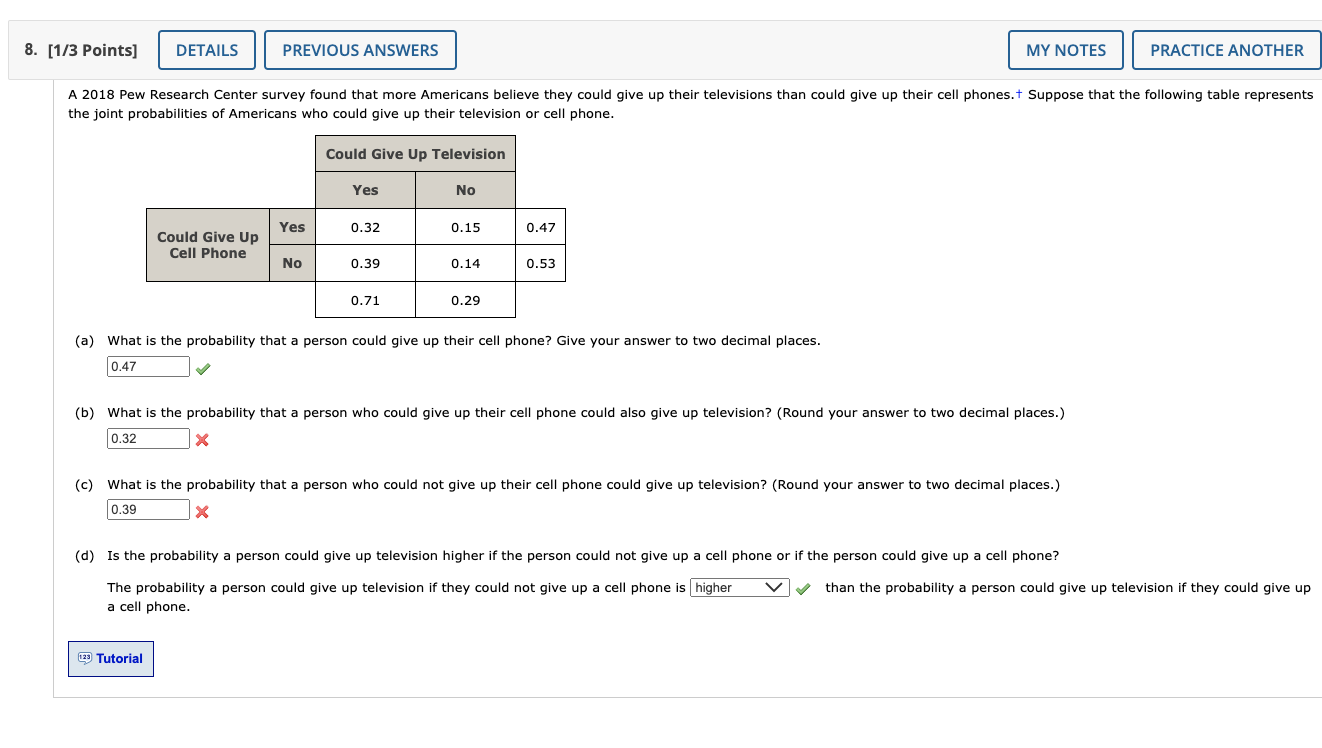
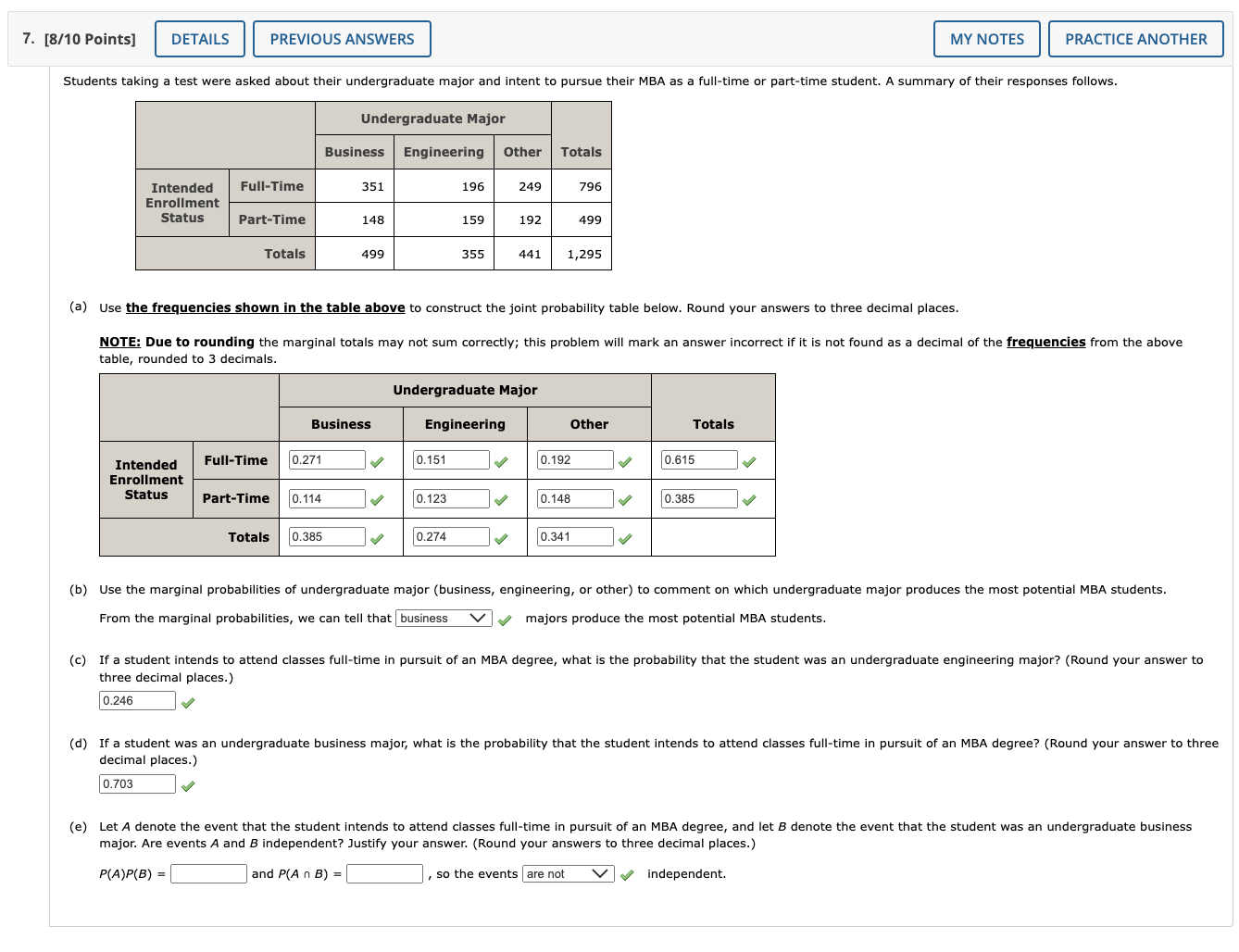
1. [4.25/5.75 Points] DETAILS PREVIOUS ANSWERS Suppose that we have a sample space with five equally likely experimental outcomes: E1, E2, E3, E4, E5. A = {E2, E4} B = {E1, E3} C = {E, E4, E5}. (a) Find P(A), P(B), and P(C). Give your answers to 1 decimal place. P(A) = 0.4 P(B) = 0.4 P(C) = 0.6 (b) Find P(A U B). Give your answer to 1 decimal place. P(AUB) = 0.8 Let MY NOTES PRACTICE ANOTHER Are A and B mutually exclusive? They are mutually exclusive. (c) Find AC. (Enter your answer in set notation. That is, use curly braces and separate the elements using commas. Use the "Functions" tab in the mathPad to correctly enter the subscripts for each element.) AC = {E1,E3,E5} Find CC. (Enter your answer in set notation. That is, use curly braces and separate the elements using commas. Use the "Functions" tab in the mathPad to correctly enter the subscripts for each element.) c-(E2,E3) Find P(A) and P(CC). Give your answers to 1 decimal place. P(AC) 0.6 P(C) = 0.4 (d) Find A U BC. (Enter your answer in set notation. That is, use curly braces and separate the elements using commas. Use the "Functions" tab in the mathPad to correctly enter the subscripts for each element.) AUBC {E2,E4,E5} Find P(A U BC). Give your answer to 1 decimal place. P(AUB) = 0.6 (e) Find P(BU C). Give your answer to 1 decimal place. P(BUC)=0.8 2. [3.5/6.5 Points] DETAILS PREVIOUS ANSWERS Suppose that we have a sample space S = {E1, E2, E3, E4, E5, E6, E7), where E1, E2, MY NOTES PRACTICE ANOTHER E, denote the sample points. The following probability assignments apply: P(E) = 0.25, P(E2) = 0.20, P(E3) = 0.15, P(E4) = 0.05, P(E5) = 0.05, P(E6) = 0.20, and P(E7) = 0.10. Let A = {E1, E4, E6} B = {E2, E4, E7} C = {E2, E31 E5, E7}. (a) Find P(A), P(B), and P(C). Give your answer to 2 decimal places. P(A) = 0.5 P(B) = 0.35 P(C) = 0.5 (b) Find A U B. (Enter your answer in set notation. That is, use curly braces and separate the elements using commas. Use the "Functions" tab in the mathPad to correctly enter subscripts for each element.) AUB=0.8 Find P(A U B). Give your answer to 2 decimal places. P(A U B) = 0.8 (c) Find An B. (Enter your answer in set notation. That is, use curly braces and separate the elements using commas. Use the "Functions" tab in the mathPad to correctly enter subscripts for each element.) AnB = {E4} Find P(A n B). Give your answer to 2 decimal places. P(A n B) = 0.05 (d) Are events A and C mutually exclusive? They are mutually exclusive. (e) Find BC. (Enter your answer in set notation. That is, use curly braces and separate the elements using commas. Use the "Functions" tab in the mathPad to correctly enter subscripts for each element.) BC= {E1,E3,E5,E6} Find P(B). Give your answer to 2 decimal places. P(B) = 0.65 Tutorial 5. [4/6 Points] DETAILS PREVIOUS ANSWERS MY NOTES PRACTICE ANOTHER High school seniors with strong academic records apply to the nation's most selective colleges in greater numbers each year. Because the number of slots remains relatively stable, some colleges reject more early applicants. Suppose that for a recent admissions class, an Ivy League college received 2,857 applications for early admission. Of this group, it admitted 1,034 students early, rejected 858 outright, and deferred 965 to the regular admission pool for further consideration. In the past, this school has admitted 18% of the deferred early admission applicants during the regular admission process. Counting the students admitted early and the students admitted during the regular admission process, the total class size was 2,371. Let E, R, and D represent the events that a student who applies for early admission is admitted early, rejected outright, or deferred to the regular admissions pool. (a) Use the data to estimate P(E), P(R), and P(D). (Round your answers to four decimal places.) P(E) = 0.3619 P(R) 0.3003 P(D) 0.3378 (b) Are events E and D mutually exclusive? They are mutually exclusive. Find P(E n D). (If necessary, round your answer to four decimal places.) P(En D) = 0 (c) For the 2,371 students who were admitted, what is the probability that a randomly selected student was accepted during early admission? (Round your answer to four decimal places.) 0.5094 (d) Suppose a student applies for early admission. What is the probability that the student will be admitted for early admission or be deferred and later admitted during the regular admission process? (Round your answer to four decimal places.) 0.6997 8. [1/3 Points] DETAILS PREVIOUS ANSWERS MY NOTES PRACTICE ANOTHER A 2018 Pew Research Center survey found that more Americans believe they could give up their televisions than could give up their cell phones.+ Suppose that the following table represents the joint probabilities of Americans who could give up their television or cell phone. Could Give Up Television Yes No Yes 0.32 0.15 Could Give Up Cell Phone 0.47 No 0.39 0.14 0.53 0.71 0.29 (a) What is the probability that a person could give up their cell phone? Give your answer to two decimal places. 0.47 (b) What is the probability that a person who could give up their cell phone could also give up television? (Round your answer to two decimal places.) 0.32 (c) What is the probability that a person who could not give up their cell phone could give up television? (Round your answer to two decimal places.) 0.39 (d) Is the probability a person could give up television higher if the person could not give up a cell phone or if the person could give up a cell phone? The probability a person could give up television if they could not give up a cell phone is higher a cell phone. than the probability a person could give up television if they could give up 123 Tutorial 7. [8/10 Points] DETAILS PREVIOUS ANSWERS MY NOTES PRACTICE ANOTHER Students taking a test were asked about their undergraduate major and intent to pursue their MBA as a full-time or part-time student. A summary of their responses follows. Undergraduate Major Business Engineering Other Totals Intended Full-Time Enrollment 351 196 249 796 Status Part-Time 148 159 192 499 Totals 499 355 441 1,295 (a) Use the frequencies shown in the table above to construct the joint probability table below. Round your answers to three decimal places. NOTE: Due to rounding the marginal totals may not sum correctly; this problem will mark an answer incorrect if it is not found as a decimal of the frequencies from the above table, rounded to 3 decimals. Undergraduate Major Business Engineering Other Totals 0.151 0.192 0.615 Intended Enrollment Status Full-Time 0.271 Part-Time 0.114 0.123 0.148 0.385 Totals 0.385 0.274 0.341 (b) Use the marginal probabilities of undergraduate major (business, engineering, or other) to comment on which undergraduate major produces the most potential MBA students. From the marginal probabilities, we can tell that business majors produce the most potential MBA students. (c) If a student intends to attend classes full-time in pursuit of an MBA degree, what is the probability that the student was an undergraduate engineering major? (Round your answer to three decimal places.) 0.246 (d) If a student was an undergraduate business major, what is the probability that the student intends to attend classes full-time in pursuit of an MBA degree? (Round your answer to three decimal places.) 0.703 (e) Let A denote the event that the student intends to attend classes full-time in pursuit of an MBA degree, and let B denote the event that the student was an undergraduate business major. Are events A and B independent? Justify your answer. (Round your answers to three decimal places.) P(A)P(B) = and P(A n B) so the events are not independent.