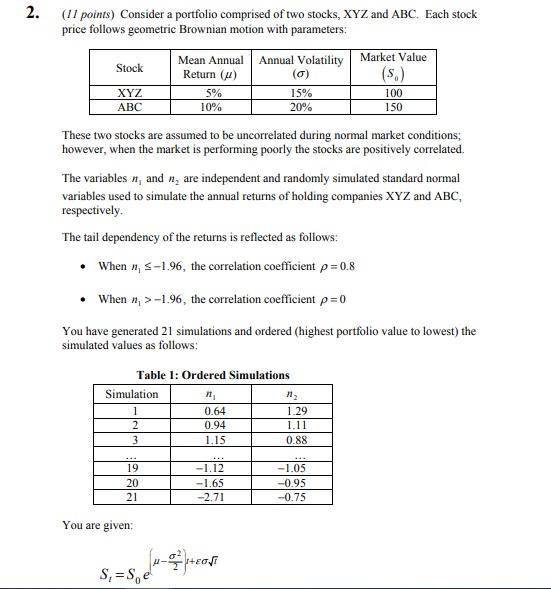
1. (8 points) Blackhawk Life is a mid-size U.S. insurer that writes both deferred variable annuities with investment performance guarantees and deferred fixed annuities. The assets backing the fixed annuities are largely invested in U.S. Treasuries and corporate bonds. The variable annuity guarantees are dynamically hedged using a combination of equity options, equity futures, and interest rate swaps. Blackhawk currently has a stress testing program that runs historical scenarios simulating major market crises that have occurred. Blackhawk is considering performing sensitivity tests as well. (a) (/ point) Evaluate the advantages of analyzing stress test results for the fixed and variable blocks separately versus in aggregate. (b) (2 points) Recommend four key unidimensional sensitivity tests that Blackhawk should run to analyze the risks of its business. Justify your response. (c) (3 points) Blackhawk is also considering performing multidimensional scenario analysis. Describe two types of multidimensional prospective scenarios. (i) Explain the drawbacks of using each of the two types of scenarios identified in (i). (iii) Recommend one scenario of each type in (i) that would be meaningful to Blackhawk. Justify your response. (d) (2 points) Blackhawk reviews the stress testing results for the October 1987 Market Crash scenario and determines that these are unacceptable. As a result, Blackhawk proposes the following two approaches to manage the risks associated with severe equity market declines: (i) De-risk the product portfolio by changing product design (ii) Hold sufficient capital Describe the consequences for each of (i) and (ii).2. (1 1 points) Consider a portfolio comprised of two stocks, XYZ and ABC. Each stock price follows geometric Brownian motion with parameters: Stock Mean Annual Annual Volatility Market Value Return (#) XYZ 5% 5% 100 ABC 10% 20% 150 These two stocks are assumed to be uncorrelated during normal market conditions; however, when the market is performing poorly the stocks are positively correlated. The variables n, and n, are independent and randomly simulated standard normal variables used to simulate the annual returns of holding companies XYZ and ABC, respectively. The tail dependency of the returns is reflected as follows: . When n, S-1.96, the correlation coefficient p = 0.8 When n, >-1.96, the correlation coefficient p =0 You have generated 21 simulations and ordered (highest portfolio value to lowest) the simulated values as follows: Table 1: Ordered Simulations Simulation 0.64 1.29 0.94 1.15 0.88 19 -1.12 -1.05 20 -1.65 -0.95 21 -2.71 -0.75 You are given: S,=Se(a) (J.5 points) Given the following formula: (i) Solve for 6, and E,. (ii) Explain the purpose of this formula and how it works. (b) (3 points) Determine the one year VaR(95%) for the portfolio value. Show your work. (c) (2 points) Evaluate in qualitative terms (without performing additional calculations) the effect that each of the following changes would have on the VaR(95%) of the portfolio. (i) The correlation coefficient increases from 0.8 to 0.9 when n 5-1.96 (ii) Tail dependency is reflected when n, S-2.65 rather than when n S-1.96 (d) (3 points) Explain the steps required to determine VaR(95%) for the portfolio value using the antithetic variable reduction technique. (e) (1.5 points) Describe two additional variance reduction techniques and evaluate whether each is appropriate to use when modeling correlated equities