Answered step by step
Verified Expert Solution
Question
1 Approved Answer
1. A bus is travelling along a straight road at 25 m/s (90 km/h) when the driver sees a deer on the road and slams
1. A bus is travelling along a straight road at 25 m/s (90 km/h) when the driver sees a deer on the road and slams on the breaks. This causes a constant deceleration (a negative acceleration) ofk m/s^2. It takes the bus 5 seconds to stop. How far does the bus travel before coming to a stop?
Let t=0 at the moment the bus driver slams on the breaks.
Let v(t) be the velocity of the bus at time t(measured in m/s).
Let s(t) be the position of the bus at time t (measured in meters), and let's choose s(0)=0.
a. Find v(0) in m/s
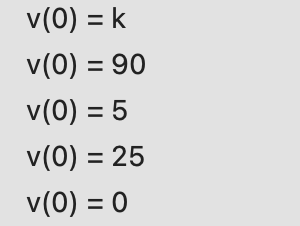







Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


