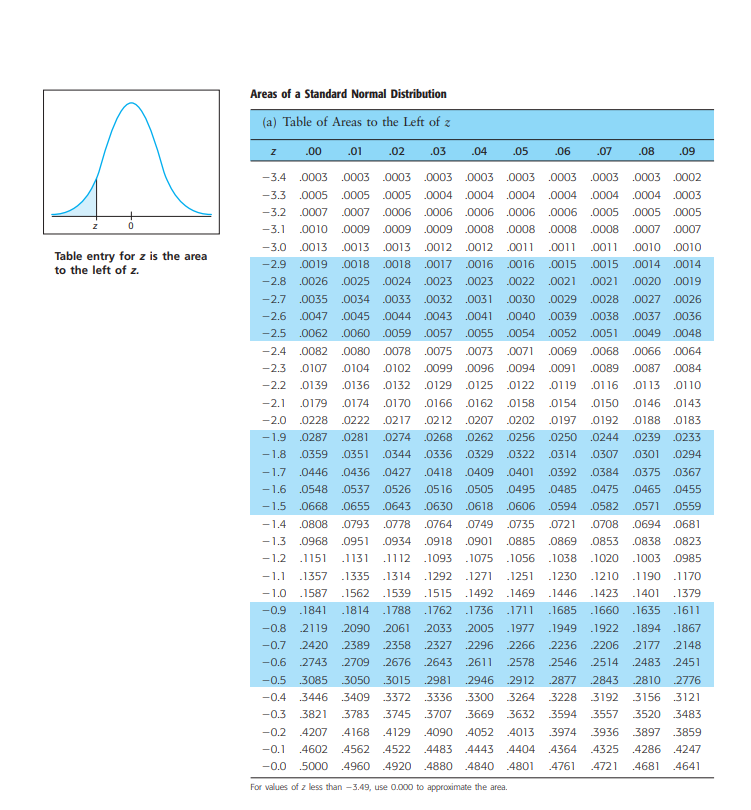
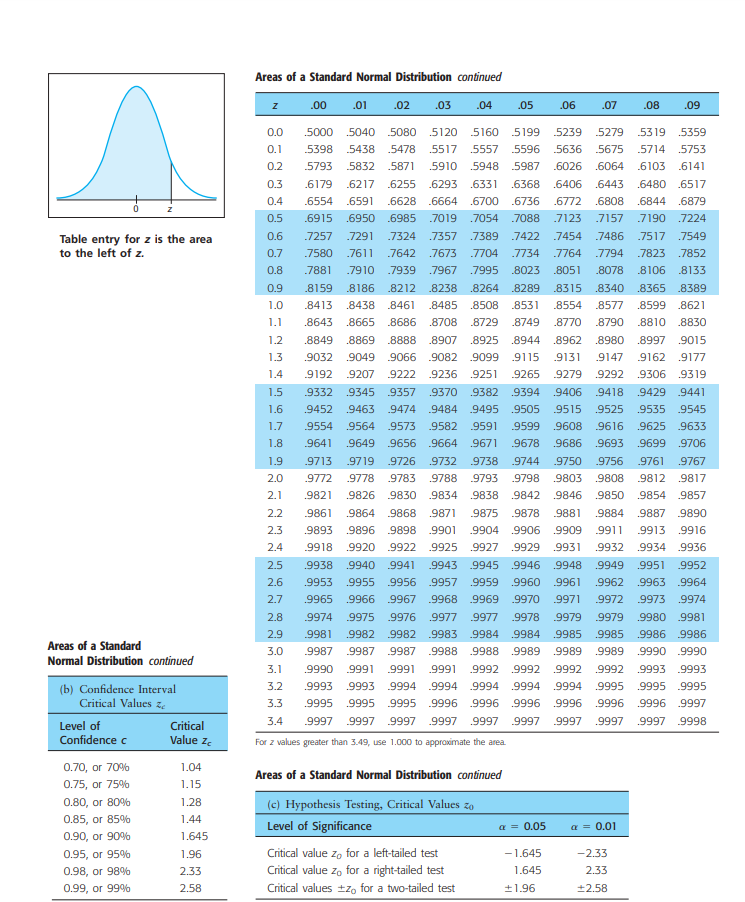
1. A large furniture store has begun a new ad campaign on local television. Before the campaign , the long-term average daily sales were $24,819. A random sample of 40 days during the new ad campaign gave a sample mean daily average sale of $25,910 Does this indicate that the population mean daily sales are now more than $24,819. Test the claim at the 1% level and assume the population standard deviation is $1917?(use the z).Areas of a Standard Normal Distribution (a) Table of Areas to the Left of z Z 00 01 .02 .03 .04 05 06 .07 08 .09 -3.4 .0003 .0003 .0003 .0003 .0003 .0003 .0003 .0003 .0003 .0002 -3.3 .0005 .0005 .0005 .0004 .0004 .0004 .0004 .0004 .0004 0003 -3.2 .0007 .0007 .0006 .0006 0006 .0006 .0006 .0005 .0005 0005 -3.1 0010 .0009 .0009 .0009 0008 .0008 .0008 .0008 .0007 0007 -3.0 0013 0013 0013 .0012 0012 0011 .0011 0011 0010 0010 Table entry for z is the area -2.9 0019 0018 .0018 .0017 .0016 .0016 0015 0015 0014 .0014 to the left of z. -2.8 .0026 .0025 .0024 .0023 .0023 .0022 .0021 .0021 .0020 .0019 - 2.7 .0035 .0034 .0033 .0032 .0031 .0030 .0029 .0028 .0027 .0026 -2.6 .0047 .0045 .0044 .0043 0040 .0039 .0038 .0037 .0036 -2.5 .0062 .0060 .0059 .0057 .0055 .0054 .0052 .0051 .0049 .0048 -2.4 .0082 .0080 .0078 .0075 -0073 .0071 .0069 .0068 .0066 0064 -2.3 0107 .0104 .0102 .0099 .0096 .0094 0091 .0089 0087 0084 -2.2 0139 .0136 .0132 .0129 .0125 .0122 0119 .0116 0113 0110 -2.1 0179 .0174 .0170 .0166 0162 0158 .0154 0150 0146 .0143 -2.0 0228 .0222 .0217 .0212 .0207 .0202 .0197 .0192 .0188 .0183 -1.9 .0287 .0281 .0274 .0268 .0262 .0256 .0250 .0244 .0239 .0233 - 1.8 .0359 .0351 0344 .0336 .0329 0322 .0314 .0307 .0301 0294 -1.7 .0446 .0436 .0427 .0418 .0409 .0401 .0392 .0384 .0375 0367 -1.6 .0548 .0537 .0526 .0516 .0505 .0495 .0485 .0475 .0465 . -1.5 .0668 .0655 .0643 0630 0618 .0606 .0594 .0582 0571 0559 -1.4 .0808 .0793 .0778 .0764 0749 0735 .0721 0708 .0694 0681 -1.3 .0968 .0951 0934 .0918 .0901 .0885 .0869 .0853 .0838 .0823 -1.2 -1151 .1131 .11 12 .1093 -1075 .1056 -1038 -1020 -1003 .0985 -1.1 -1357 .1335 . 1314 1292 1271 .1251 1230 .1210 .1190 .1170 -1.0 .1587 -1562 . 1539 . 1515 .1492 -1469 .1446 -1423 -1401 .1379 -0.9 .1841 .1814 .1788 .1762 -1736 .1711 .1685 -1660 .1635 .1611 -0.8 .2119 .2090 2061 .2033 .2005 . 1977 .1949 .1922 .1894 .1867 -0.7 2420 .2389 .2358 .2327 .2296 2266 2236 2206 .2177 .2148 -0.6 .2743 .2709 .2676 .2643 .2611 .2578 2546 2514 .2483 .2451 -0.5 .3085 3050 .3015 .2981 .2946 .2912 .2877 .2843 .2810 .2776 -0.4 3446 .3409 .3372 .3336 .3300 3264 3228 3192 3156 .3121 -0.3 3821 3783 .3745 .3707 .3669 3632 3594 3557 3520 .3483 -0.2 -4207 .4168 .4129 4090 .4052 4013 .3974 3936 3897 .3859 -0.1 .4602 .4562 4522 4483 4443 .4404 .4364 4325 .4286 .4247 -0.0 .5000 .4960 4920 4880 4840 4801 .4761 .4721 .4681 .4641 For values of z less than -3.49, use 0.000 to approximate the areaAreas of a Standard Normal Distribution continued Z .00 .01 .02 .03 .04 .05 .06 .07 .08 .09 0.0 .5000 5040 5080 .5120 5160 .5199 .5239 .5279 .5319 .5359 0. 1 5398 5438 .5478 .5517 .5557 5596 .5636 .5675 .5714 .5753 0.2 .5793 5832 .5871 .5910 .5948 -5987 -6026 .6064 6103 .6141 0.3 6179 6217 .6255 .6293 .6331 6368 .6406 .6443 .6480 .6517 0.4 .6554 6591 .6628 .6664 .6700 -6736 .6772 .6808 .6844 .6879 0.5 .6915 .6950 .6985 7019 .7054 .7088 .7123 .7157 7190 .7224 Table entry for z is the area 0.6 .7257 .7291 .7324 .7357 .7389 .7422 .7454 .7486 .7517 .7549 to the left of z. 0.7 .7580 .7611 .7642 .7673 .7704 .7734 .7764 .7794 .7823 .7852 0.8 .7881 .7910 .7939 .7967 .7995 .8023 8051 .8078 -8106 .8133 0.9 .8159 8186 8212 .8238 .8264 8289 .8315 .8340 .8365 .8389 1.0 .8413 .8438 8461 .8485 .8508 .8531 .8554 .8577 .8599 .8621 1. 1 .8643 .8665 .8686 .8708 8729 .8749 .8770 .8790 -8810 .8830 1.2 .8849 .8869 .8888 .8907 .8925 .8944 .8962 .8980 .8997 .9015 1.3 .9032 9049 .9066 .9082 .9099 .9115 9131 9147 9162 .9177 1.4 9192 .9207 .9222 .9236 .9251 .9265 .9279 .9292 .9306 .9319 1.5 .9332 .9345 .9357 .9370 .9382 .9394 .9406 9418 .9429 .9441 1.6 .9452 .9463 9474 .9484 .9495 .9505 -9515 .9525 .9535 .9545 1.7 9554 .9564 .9573 .9582 .9591 .9599 .9608 9616 .9625 .9633 18 .9641 9649 9656 .9664 .9671 .9678 .9686 .9693 9699 .9706 1.9 .9713 .9719 .9726 .9732 .9738 .9744 .9750 .9756 .9761 .9767 2.0 .9772 .9778 .9783 .9788 .9793 9798 9803 9808 9812 .9817 2. 1 9821 9826 .9830 .9834 .9838 9842 9846 9850 .9854 .9857 2.2 9861 9864 .9868 .9871 .9875 -9878 9881 .9884 .9887 .9890 2.3 9893 9896 9898 .9901 .9904 .9906 .9909 9911 9913 .9916 2.4 9918 .9920 -9922 .9925 .9927 .9929 .9931 9932 .9934 .9936 2.5 .9938 .9940 .9941 .9943 .9945 .9946 .9948 .9949 .9951 .9952 2.6 .9953 .9955 .9956 .9957 .9959 .9960 -9961 .9962 .9963 .9964 27 9965 9966 .9967 .9968 9969 9970 9971 .9972 .9973 .9974 2.8 9974 .9975 .9976 .9977 .9977 -9978 .9979 9979 .9980 .9981 2.9 9981 9982 9982 .9983 9984 .9984 .9985 9985 9986 .9986 Areas of a Standard 3.0 .9987 9987 .9987 .9988 .9988 .9989 .9989 9989 .9990 .9990 Normal Distribution continued 31 9990 9991 9991 9991 .9992 .9992 .9992 .9992 .9993 .9993 (b) Confidence Interval 3.2 9993 .9993 .9994 .9994 .9994 .9994 .9994 9995 .9995 .9995 Critical Values & 3.3 9995 .9995 .9995 -9996 .9996 .9996 .9996 9996 .9996 .9997 9997 .9997 9997 .9997 .9997 9997 .9997 .9997 9997 9998 Level of Critical Confidence c Value Z For z values greater than 3.49, use 1.000 to approximate the area. 0.70, or 70% 1.04 Areas of a Standard Normal Distribution continued 0.75, or 75% 1.15 0.80, or 80% 1.28 (c) Hypothesis Testing, Critical Values zo 0.85, or 85% 1.44 Level of Significance 4 = 0.05 1 = 0.01 0.90, or 909% 1.645 0.95, or 95% 1.96 Critical value zo for a left-tailed test -1.645 -2.33 0.98, or 98% 2.33 Critical value zo for a right-tailed test 1.645 2.33 0.99, or 99% 2.58 Critical values +zo for a two-tailed test +1.96 +2.58