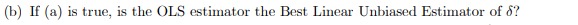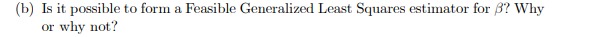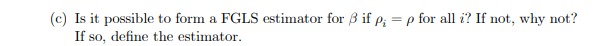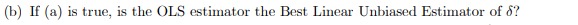




1. A latent variable y* is related to a (scalar) covariate a by yi = Pot Biritei, where &; is independently and identically distributed as a Uniform random variable on the interval [-a, a], a > 0. Recall that the probability density function (p.d.f.) of e in this case is f (E) = 2a for a E [-a, a], and the cumulative distribution function is F(8) = (e + a)/(2a) for a e [-a, a]. Assume that you have access to a random sample of N observations, {ya, m} where Vi if y; > 0 You estimate the linear regression model (yi - .5) = 60 + diri + wi by Ordinary Least Squares. Denote the OLS estimates of & by 5. (a) In the linear regression model. is E(6) = 6?(b) If (a) is true, is the OLS estimator the Best Linear Unbiased Estimator of 6?(c) We aren't really interested in the parameters o. Determine whether E61 = B1- If not, what additional information would you need to be able to define an unbiased estimator of S, (in addition to 61)?2. lIDEIInsider the panel data regression model Elli-t = JET-Ti: + Err where $11 = PiEitl -l- "at: and where a\" is i.i.d. with mean and variance 03,, and where |p,| s: 1 for all i, and the p,- are unknown. You have aooess to a random sample of observations from the population for N individuals and 2 time periods, {y,$,1},-=1,___1N,=11g. We assume that an: is a scalar for simplicity, and that all variables are measured as deviations from their means. [a] Using; both time periods of data, dene the ULS estimator of ,8. Determine whether the 0L3 estimator is unbiased. (b) Is it possible to form a Feasible Generalized Least Squares estimator for ? Why or why not?(c) Is it possible to form a FGLS estimator for 8 if p; = p for all i? If not, why not? If so, define the estimator.4. A cross-sectional population regression model is given by yi = Britei, where y; and ; are expressed as deviations from their respective means, and &; is independently and identically distributed (i.i.d.) with mean 0 and variance oz. You have access to a random sample of observations on {yar}_ IN. The variable r* is a "noisy" measure of r;, that is, m=ritui, where u; is i.i.d. with mean 0 and variance o? > 0. (a) Say that you form the estimator Show that plim 6 / B.(b) Say that you have access to another variable {} ], which is also expressed as a deviation from its mean, that has the following properties in the population: E(zx) / 0 E(Ez) = 0. With this variable, can you define a consistent estimator of 8? If so, define it, and provide a short proof of consistency