1. a) Let f(n) = 6n² - 100n + 44 and g(n) = 0.5n³ . Prove that f(n) = O(g(n)) using the definition of Big-O notation. (You need to find constants c and n0).

b) Let f(n) = 3n² + n and g(n) = 2n² . Use the definition of big-O notation to prove that

1. f(n) = O(g(n)) (you need to find constants c and n0) and

2. g(n) = O(f(n)) (you need to find constants c and n0).

Conclude that f(n) = (g(n)).

2. Order the following 16 functions by asymptotic growth rate from lowest to highest. If any are of the same order then circle them on your list.

5n-6, 3, 5n+n³, 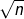, n^2.01, 3^log₂n, 4log n, n!, log n³, n^1/3, 3n³-5n+n⁴, n log n +4n, 10n⁴, 4ⁿ, 2ⁿ, 4ⁿ⁺¹. Note: When comparing two functions f(n) and g(n) you may use 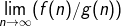to compare their asymptotic growth rates.

lim (f(n)/g(n))