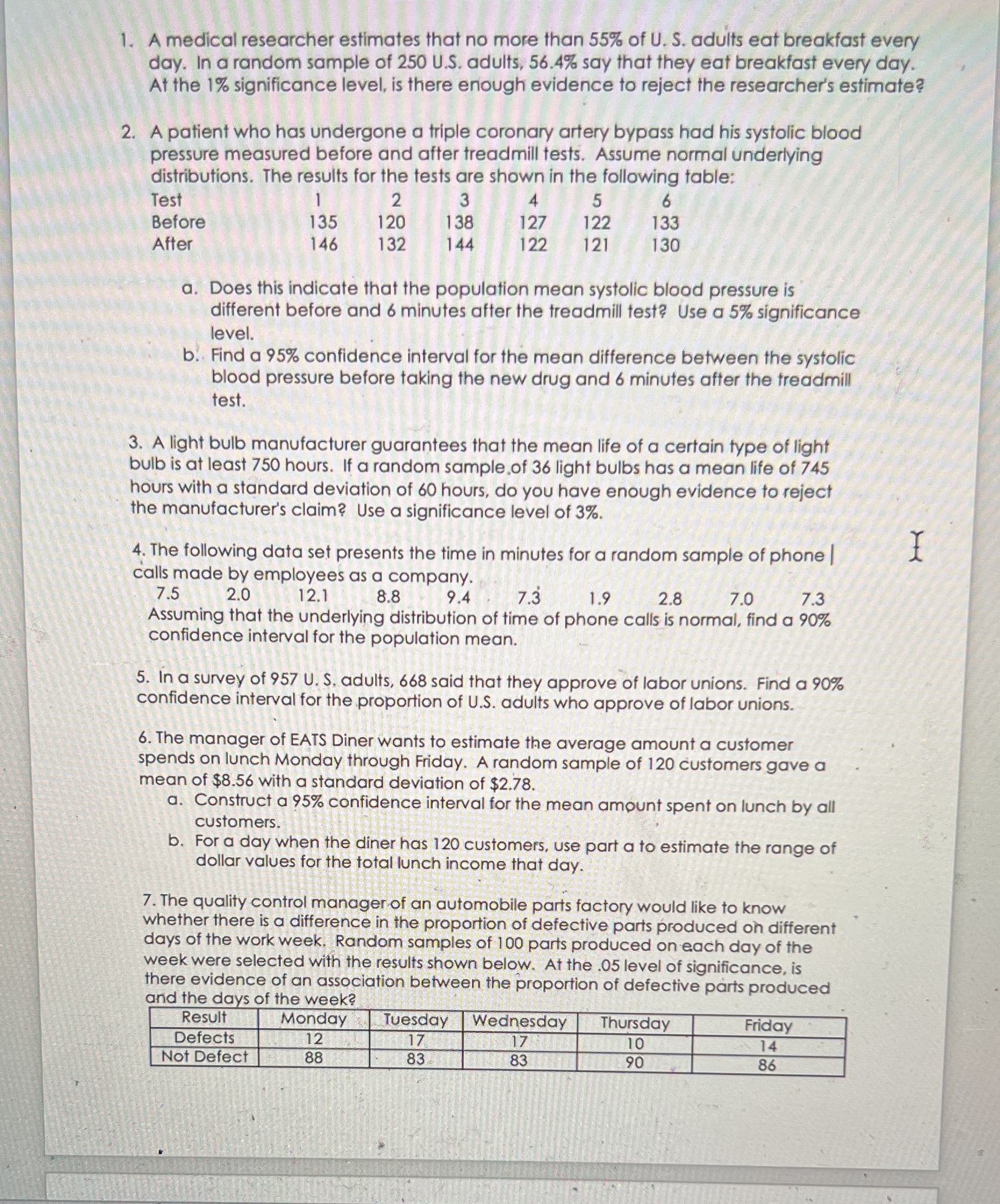
1. A medical researcher estimates that no more than 55%% of U. S. adults eat breakfast every day. In a random sample of 250 U.S. adults, 56.4% say that they eat breakfast every day. At the 1% significance level, is there enough evidence to reject the researcher's estimate? 2. A patient who has undergone a triple coronary artery bypass had his systolic blood pressure measured before and after treadmill tests. Assume normal underlying distributions. The results for the tests are shown in the following table: Test 2 3 5 Before 135 120 138 127 122 133 After 146 132 144 122 121 130 a. Does this indicate that the population mean systolic blood pressure is different before and 6 minutes after the treadmill test? Use a 5% significance level. b. Find a 95% confidence interval for the mean difference between the systolic blood pressure before taking the new drug and 6 minutes after the treadmill test . 3. A light bulb manufacturer guarantees that the mean life of a certain type of light bulb is at least 750 hours. If a random sample of 36 light bulbs has a mean life of 745 hours with a standard deviation of 60 hours, do you have enough evidence to reject the manufacturer's claim? Use a significance level of 3%. 4. The following data set presents the time in minutes for a random sample of phone | calls made by employees as a company. 7.5 2.0 12.1 8.8 9.4 7.3 1.9 2.8 7.0 7.3 Assuming that the underlying distribution of time of phone calls is normal, find a 90% confidence interval for the population mean. 5. In a survey of 957 U. S, adults, 668 said that they approve of labor unions. Find a 90% confidence interval for the proportion of U.S. adults who approve of labor unions. 6. The manager of EATS Diner wants to estimate the average amount a customer spends on lunch Monday through Friday. A random sample of 120 customers gave a mean of $8.56 with a standard deviation of $2.78. a. Construct a 95% confidence interval for the mean amount spent on lunch by all customers. b. For a day when the diner has 120 customers, use part a to estimate the range of dollar values for the total lunch income that day. 7. The quality control manager of an automobile parts factory would like to know whether there is a difference in the proportion of defective parts produced on different days of the work week. Random samples of 100 parts produced on each day of the week were selected with the results shown below. At the .05 level of significance, is there evidence of an association between the proportion of defective parts produced and the days of the week? Result Monday Tuesday Wednesday Thursday Friday Defects 12 10 14 Not Defect 88 83 83 90 86