Question
1. (a) Modify the function ex with 2eqs to solve the IVP (L4.4) for 0 t 40 using the MATLAB routine ode45. Call the new
1. (a) Modify the function ex with 2eqs to solve the IVP (L4.4) for 0 t 40 using the MATLAB routine ode45. Call the new function LAB04ex1. Let [t,Y] (note the upper case Y) be the output of ode45 and y and v the unknown functions. Use the following commands to define the ODE: function dYdt= f(t,Y) y=Y(1); v=Y(2); dYdt = [v; cos(t)-4*v-3*y]; Plot y(t) and v(t) in the same window (do not use subplot), and the phase plot showing v vs y in a separate window. Add a legend to the first plot. (Note: to display v(t) = y (t), use v(t)=y(t)). Add a grid. Use the command ylim([-1.5,1.5]) to adjust the y-limits for both plots. Adjust the x-limits in the phase plot so as to reproduce the pictures in Figure L4g. Include the M-file in your report.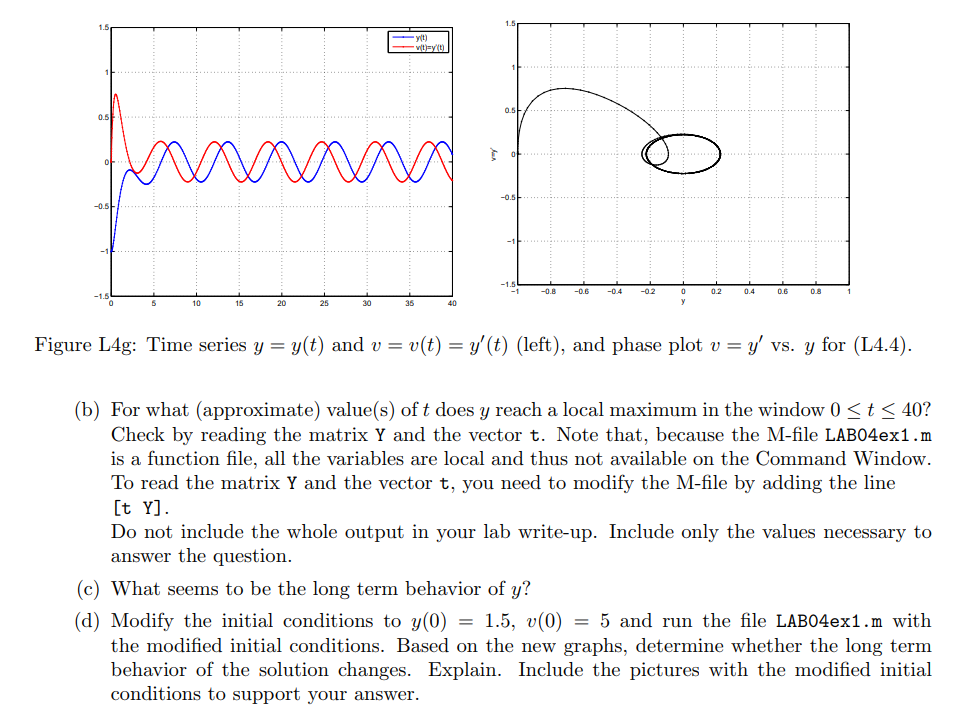

Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


