1. A physical education teacher observes a strong and linear relationship between the number of sit-ups a student can do in one minute and the amount of time it takes the student, in seconds, to complete a 40-yard dash. If the physical education teacher wants to predict amount of time to complete a 40-yard dash based on number of sit-ups that can be completed in one minute, which variable should go on the vertical (or y) axis of the scatterplot?

Choose the correct answer

A. Number of sit-ups, because it is the explanatory variable.

B. Number of sit-ups, because it is the response variable.

C. Amount of time to complete the 40-yard dash, because it is the explanatory variable.

D. Amount of time to complete the 40-yard dash, because it is the response variable.

E. This question cannot be answered without knowing if the relationship is positive or negative.

2. You read the following statement in a news article: "Mothers who spend more time on social media sites about motherhood experience higher levels of a hormone known as cortisol." From this statement, we should conclude that

Choose the correct answer

A. spending more time on social media sites about motherhood causes an increase in levels of the cortisol hormone.

B. the relationship between time spent on social media sites about motherhood and levels of the cortisol hormone is positive.

C. the relationship between time spent on social media sites about motherhood and levels of the cortisol hormone is negative.

D. the relationship between time spent on social media sites about motherhood and levels of the cortisol hormone is strong.

E. the relationship between time spent on social media sites about motherhood and levels of the cortisol hormone is moderate.

3. Consider the following five statements. Given what you have learned about correlation and regression from Chapters 14 and 15, only one of these statements can be correct. Which statements is correct?

Choose the correct answer

A. The correlation between home price (in dollars) and distance of the home from the nearest school (in miles) is r = -2.75.

B. The correlation between political party affiliation and favorite ice cream flavor is r = 0.42.

C. The correlation between eye color and height is r = -0.21.

D. The correlation between number of letters in a person's name and whether or not the person likes pineapple as a pizza topping is r = 0.87.

E. The correlation between hours spent working per day and minutes spent studying per day is r = -0.69.

4. An apartment rental company compiles information about the square footage and amount of rent per month for several apartments in a large city. All of the apartments in the sample are between 485 square feet and 1800 square feet. There is a strong, positive, and linear relationship between the square footage and amount of rent (in dollars) of these apartments. The regression equation to predict amount of rent based on square footage is as follows:

Predicted rent = -162 + 2.25 (square feet)

From the above information, we can predict that an apartment that is 845 square feet will have rent per month of approximately _________ dollars.

Choose the correct answer

A. 1007.00

B. 1901.25

C. 1739.25

D. 685.25

E. 2061.25

5. This past Halloween, data was gathered from several trick-or-treaters about the amount of time they spent trick-or-treating (in minutes) and the amount of candy they obtained (in grams) while trick-or-treating. The relationship between these variables is linear and strong. The regression equation that can be used to predict amount of candy obtained from time spent trick-or-treating is:

Predicted grams of candy = 296.90 + 15.45 (minutes spent trick-or-treating)

Which one of the following statements is a correct interpretation of this regression equation?

Choose correct answer

A. As minutes spent trick-or-treating goes up by one, we predict grams of candy to increase by 296.90.

B. As minutes spent trick-or-treating goes up by one, we predict grams of candy to increase by 15.45.

C. As grams of candy goes up by one, we predict minutes spent trick-or-treating to increase by 296.90.

D. As grams of candy goes up by one, we predict minutes spent trick-or-treating to increase by 15.45.

E. 15.45% of the variability in grams of candy can be explained by the regression equation.

6. Scientists have observed a relationship between the number of times a cricket chirps, per minute, and the temperature, measured in degrees Fahrenheit. As the temperature increases, crickets appear to chirp more, per minute. The relationship between temperature and number of cricket chirps per minute is linear, with r = 0.84, and the equation that can be used to predict temperature based on number of cricket chirps per minute is as follows:

Predicted temperature = 25.2 + 3.29 (number of cricket chirps per minute)

From the above information, we know that approximately _____% of the variability in temperature can be explained by the regression equation.

choose correct answer

A. 70.56

B. 84.00

C. 91.65

D. 42.00

E. 16.80

7. Return to Question 6. If the units of temperature were measured in degrees Celsius rather than in degrees Fahrenheit, how would you expect the correlation between temperature and number of cricket chirps per minute to change?

Choose correct answer

A. The correlation would become stronger.

B. The correlation would become weaker.

C. The correlation would become negative.

D. The correlation would become weaker and negative.

E. The correlation would not change at all.

8. If there is a linear, strong, and negative relationship between the scores on two tests, we should conclude that

Choose the correct answer

A. high scores on one test are associated with high scores on the other test.

B. high scores on one test are associated with low scores on the other test.

C. the value of r must be close to 0.

D. as one test score goes down, the other test score goes down.

E. scoring high on one test causes an individual to score low on the other test.

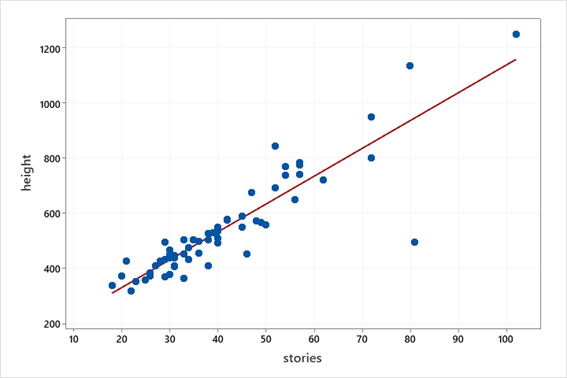
9. Is the height of a building, measured in feet, related to the number of stories the building has? Data was gathered from a random sample of 60 tall buildings in the United States, and this data is presented in the scatterplot below. The correlation between height and number of stories was observed to be r = 0.89, and the equation to predict height based on number of stories is given below.

Predicted height = 129.8 + 10.10 (stories)

1200 1000 800 height 600 400 200 10 20 30 40 50 60 70 80 90 100 stories