



1.
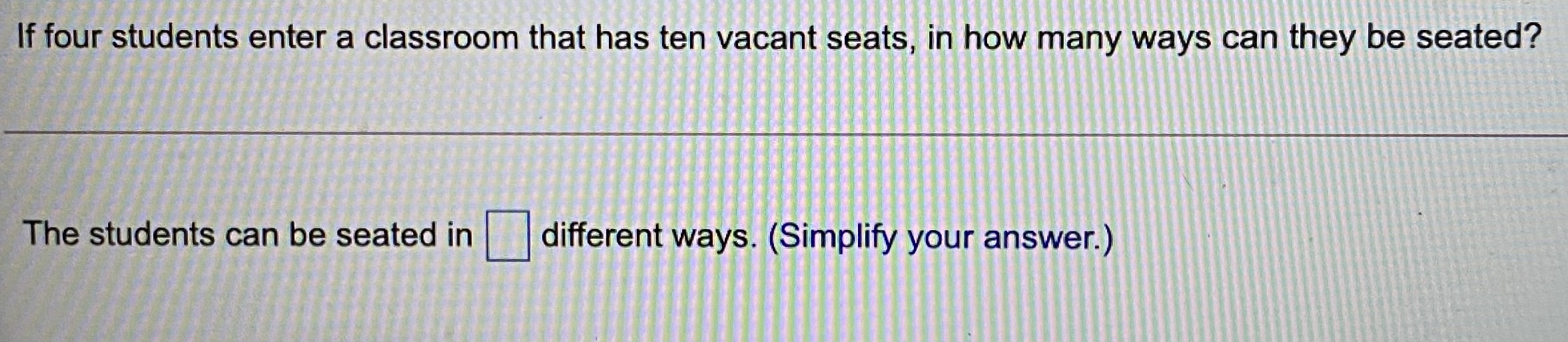
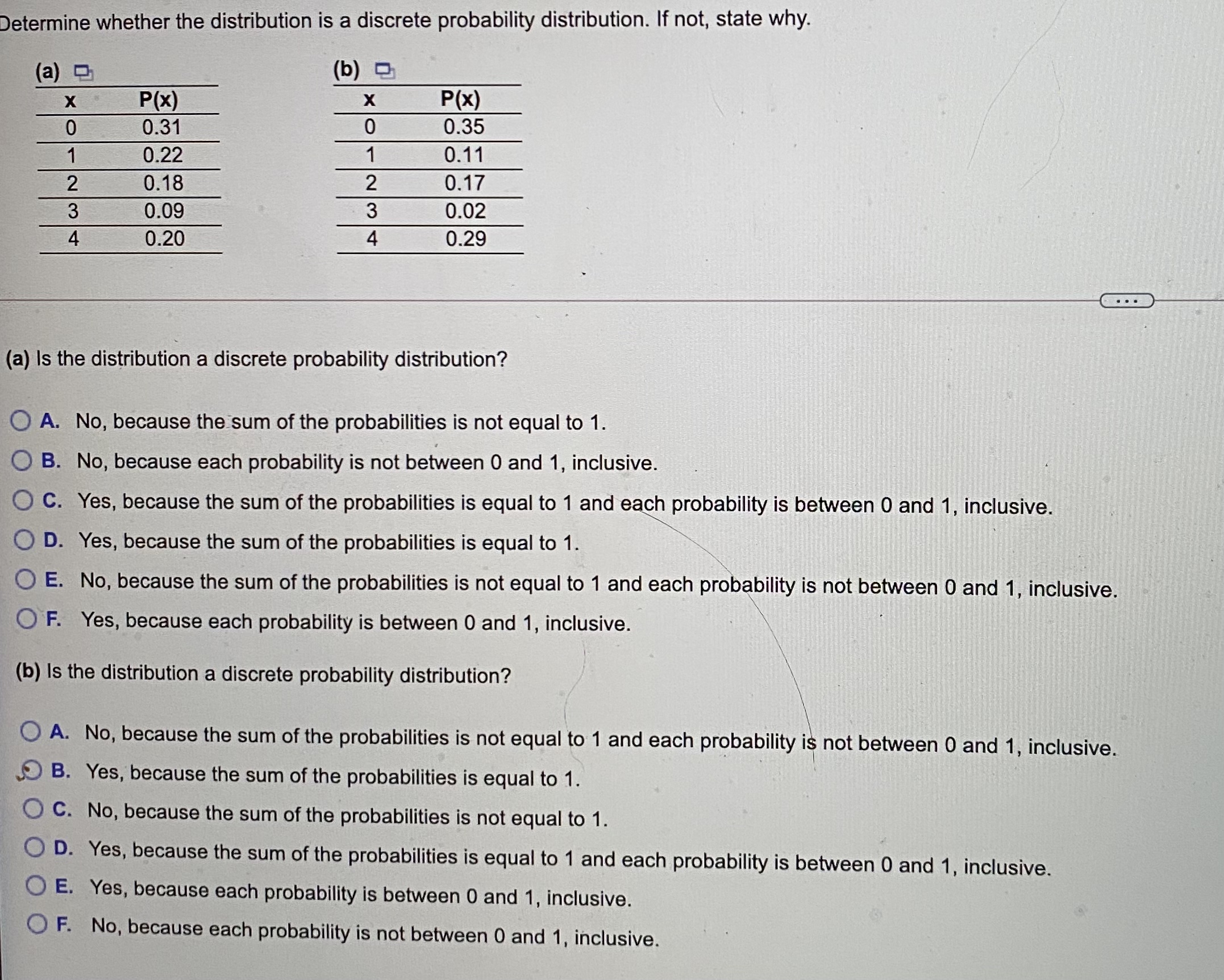
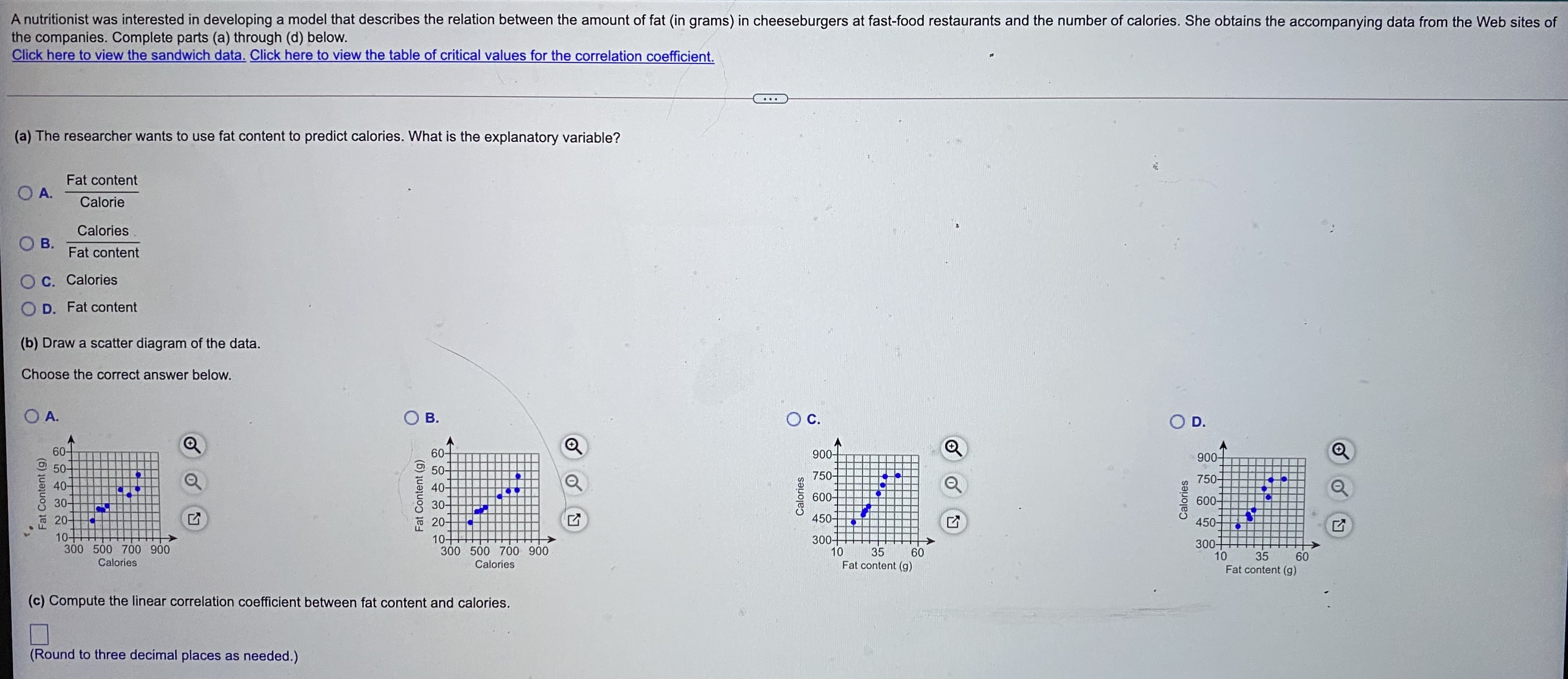
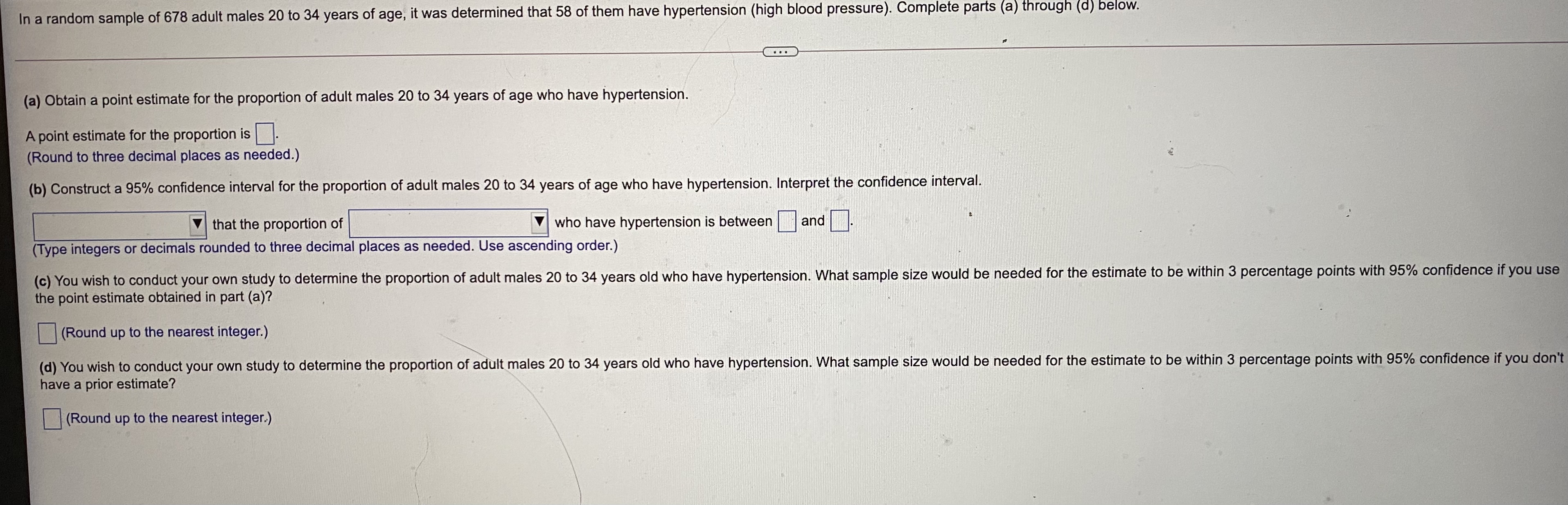
An insurance company crashed four cars in succession at 5 miles per hour. The cost of repair for each of the four crashes was $420, $459, $406, $237 3 . Compute the range, sample variance, and sample standard deviation cost of repair. The range is $ $2 = ]dollars2 (Round to the nearest whole number as needed.) s = $ (Round to two decimal places as needed.)If four students enter a classroom that has ten vacant seats, in how many ways can they be seated? The students can be seated in different ways. (Simplify your answer.)10# 300 500 700 900 300 500 700 10 35 60 10 35 60 Calories Calories Fat content (9) Fat content (9) (c) Compute the linear correlation coefficient between fat content and calories. (Round to three decimal places as needed.) (d) Does a linear relation exist between fat content and calories in the fast-food restaurant sandwiches? A linear relation between fat content and calories in the fast-food restaurant sandwiches, since the scatter diagram a linear relation and the absolute value of the linear correlation coefficient is the critical value. (Round to three decimal places as needed.)Determine whether the distribution is a discrete probability distribution. If not, state why. (a) (b) X P(X X P(x) 0 0.31 0 0.35 1 0.22 1 0.11 2 0.18 2 0.17 3 0.09 3 0.02 4 0.20 4 0.29 (a) Is the distribution a discrete probability distribution? O A. No, because the sum of the probabilities is not equal to 1. O B. No, because each probability is not between 0 and 1, inclusive. C. Yes, because the sum of the probabilities is equal to 1 and each probability is between 0 and 1, inclusive. O D. Yes, because the sum of the probabilities is equal to 1. O E. No, because the sum of the probabilities is not equal to 1 and each probability is not between 0 and 1, inclusive. OF. Yes, because each probability is between 0 and 1, inclusive. (b) Is the distribution a discrete probability distribution? A. No, because the sum of the probabilities is not equal to 1 and each probability is not between 0 and 1, inclusive. B. Yes, because the sum of the probabilities is equal to 1. O C. No, because the sum of the probabilities is not equal to 1. O D. Yes, because the sum of the probabilities is equal to 1 and each probability is between 0 and 1, inclusive. O E. Yes, because each probability is between 0 and 1, inclusive. OF. No, because each probability is not between 0 and 1, inclusive.A simple random sample of size n = 46 is obtained from a population that is skewed left with u = 60 and o = 7. Does the population need to be normally distributed for the sampling distribution of x to be approximately normally distributed? Why? What is the sampling distribution of x? Does the population need to be normally distributed for the sampling distribution of x to be approximately normally distributed? Why? A. No. The central limit theorem states that regardless of the shape of the underlying population, the sampling distribution of x becomes approximately normal as the sample size, n, increases. O B. Yes. The central limit theorem states that the sampling variability of nonnormal populations will increase as the sample size increases. O C. Yes. The central limit theorem states that only for underlying populations that are normal is the shape of the sampling distribution of x normal, regardless of the sample size, n. D. No. The central limit theorem states that only if the shape of the underlying population is normal or uniform does the sampling distribution of x become approximately normal as the sample size, n, increases. What is the sampling distribution of x? Select the correct choice below and fill in the answer boxes within your choice. (Type integers or decimals rounded to three decimal places as needed.) A. The sampling distribution of x is skewed left with u = |and ox = O B. The shape of the sampling distribution of x is unknown with u = |and o =. O C. The sampling distribution of x is uniform with My = |and ox =. O D. The sampling distribution of x is approximately normal with ux = and ox =A nutritionist was interested in developing a model that describes the relation between the amount of fat (in grams) in cheeseburgers at fast-food restaurants and the number of calories. She obtains the accompanying data from the Web sites of the companies. Complete parts (a) through (d) below. Click here to view the sandwich data. Click here to view the table of critical values for the correlation coefficient. (a) The researcher wants to use fat content to predict calories. What is the explanatory variable? Fat content O A Calorie Calories O B. Fat content O c. Calories O D. Fat content (b) Draw a scatter diagram of the data. Choose the correct answer below. O A. OB. O c. OD. 60- 60 900 50- 750- 40 Calories 600- Calories 600- 30- Fat C 20- TO 20- 450- 450- 10- 300- 300 500 700 900 300 500 700 900 10 35 60 10 35 60 Calories Calories Fat content (9) Fat content (9) (c) Compute the linear correlation coefficient between fat content and calories. (Round to three decimal places as needed.)In a random sample of 678 adult males 20 to 34 years of age, it was determined that 58 of them have hypertension (high blood pressure). Complete parts (a) through (d) below. (a) Obtain a point estimate for the proportion of adult males 20 to 34 years of age who have hypertension. A point estimate for the proportion is. (Round to three decimal places as needed.) (b) Construct a 95% confidence interval for the proportion of adult males 20 to 34 years of age who have hypertension. Interpret the confidence interval. that the proportion of who have hypertension is between and. (Type integers or decimals rounded to three decimal places as needed. Use ascending order.) (c) You wish to conduct your own study to determine the proportion of adult males 20 to 34 years old who have hypertension. What sample size would be needed for the estimate to be within 3 percentage points with 95% confidence if you use the point estimate obtained in part (a)? (Round up to the nearest integer.) (d) You wish to conduct your own study to determine the proportion of adult males 20 to 34 years old who have hypertension. What sample size would be needed for the estimate to be within 3 percentage points with 95% confidence if you don't have a prior estimate? (Round up to the nearest integer.)The student copy machine in the library requires a maintenance call an average of two times per month. Assuming that the number of required maintenance calls follows a Poisson distribution, would it be unusual for the copy machine to require more than five maintenance calls in any given month? Why or why not? Since P(X V 5) =], it be unusual to have more than 5 maintenance calls. (Round to four decimal pla would not would






















