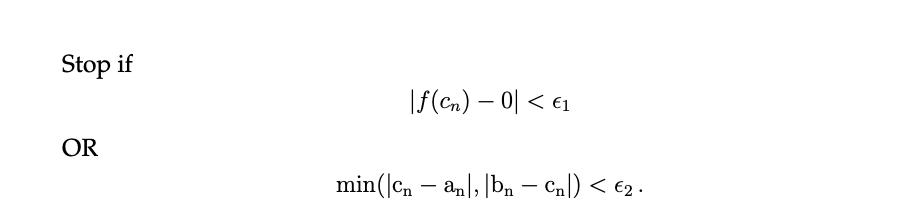
= 1 and we i) Consider the function h(x) =x sin(x). We seek to find where h(x) will do so by using the bisection method to find the root of f(x) = h(x) 1. Use the intermediate value theorem to argue that at least one root exists on the interval x = [0,2]. 0.5 f(x) A -0.5- X 2 3 Figure 2: f(x) = x sin(x) - -1 ii) Complete a table of bisection method computations for i = 0, 1, 2. a f(a) cf(c) b |f(b) [3 marks] i 00 1 2 2 [6 marks] iii) The usual tolerance test used to determine when computations should be ter- minated is f(x) 0| < e. Explain why | bn-an| Stop if OR |f(cn) - 0 < 1 min(cn an, bn - Cn|) < 2. -