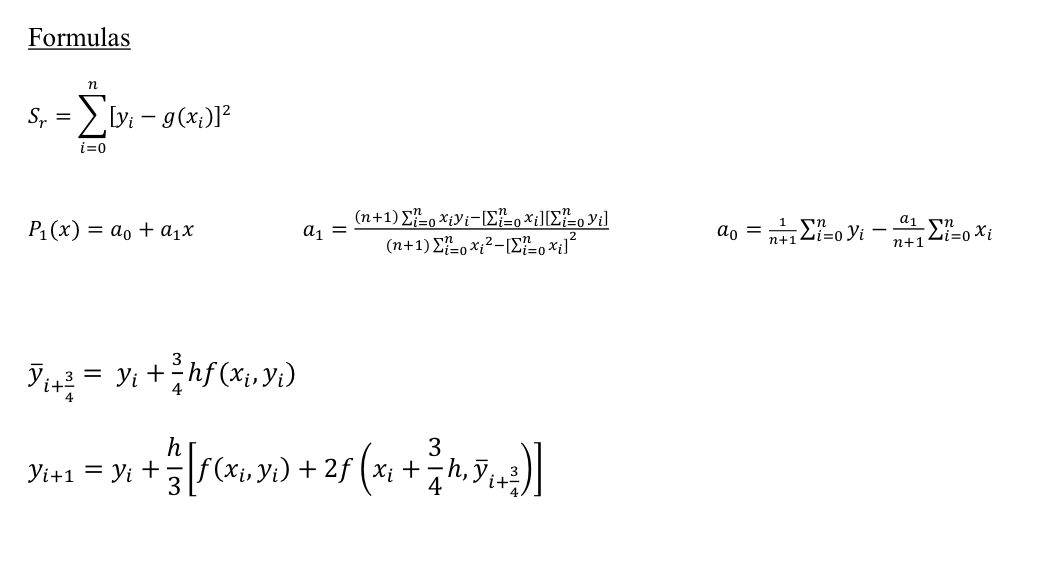
1) Assuming small deflections, the transverse vibration of two masses m, m which are equally spaced on a taut string can be described by the differential equations 3T - 7x + (x L 3T (X X) = MX L 3T - (x - -I (x-x) - 3T x = MX2 where L is the length of the string and T is the tension in the string (assumed constant). a) If the deflection vector is x = [x x], rewrite the equations of motion in the form * = Ax. b) If L = 3 m, T = 1 N, and m = m = 1 kg, find the eigenvalues and eigenvectors of A using the Power method with the Euclidean norm. Use the starting vector vo = [0.6 - 0.8]. Hint: The eigenvalues have integer values. Two iterations for each should suffice. 1/11 L/3 L/3 L/3 1 X m m Taylo 4th de RR Forward Budwud centual Formulas Vm+1 Avm ||Avm|| k = f(x, y) y(xo + h) = y(xo) + hy'(xo)+ 2y"(xo)+gy"(xo) + h 3! h Yi+1=Y + [k + 2k+2k3 + K4] h k = f(x + 2/2,V + 1/ hk) h 1 K3 = f(x+Y+2 hk ) k= f(x + h, y + hk3) du Ui+1,jui,j Ax x ~ B = A - I Ju ui,j-ui-1.j ax du Ui+1,j-ul-1,j 24x x 2u x h Ui-1,j2ui,j + U+1,j (4x) B = (A-21) (A-21) Formulas s, = vi-g(1 P1 (x) = a + aix Yug = y + 3hf(x,y) 1 = (n+1) =o Xiyi-[=oxi][=ovi] (n+1) {=ox;2[=oxi] h Vi+1 = Ji + f(xwyi) + 2f (xi + h 3 +2f(x+h5)] - n1,-oy; 1,-oxi =0 n+1