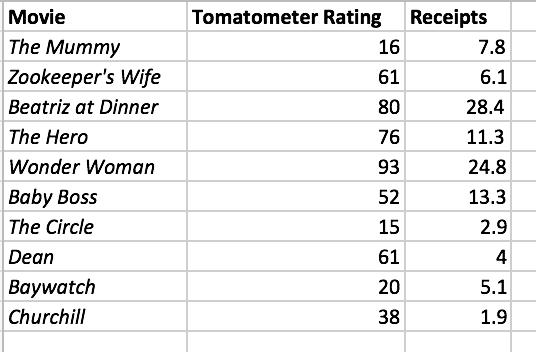
1. Can you use movie critics' opinions to forecast box office receipts on the opening weekend? The data stored in Tomatometer.xlsx (attached pic) include the Tomatometer rating, the percentage of professional critic reviews that are positive, and the receipts per theater ($thousands) on the weekend a movie opened for ten movies.

a. Use the least-squares method to get the regression coefficients b(lower power 0)and b(lower power 1). Interpret the meaning of b(lower power 0)and b(lower power 1)in this problem.

b. Predict the mean receipts for a movie that has a Tomatometer rating of 55%.

c. Determine the coefficient of determination, r^2, and explain its meaning in this problem.

d. Perform a residual analysis by plotting residuals against X and constructing the normal probability plot of residuals. Is there any evidence of a pattern in the residuals? Explain.

e. At the 0.05 level of significance, is there evidence of a linear relationship between Tomatometer rating and receipts? Explain.

f.Based on the results of part (a)-(e), do you think that Tomatometer rating is a useful predictor of receipts on the first weekend a movie opens? Explain.

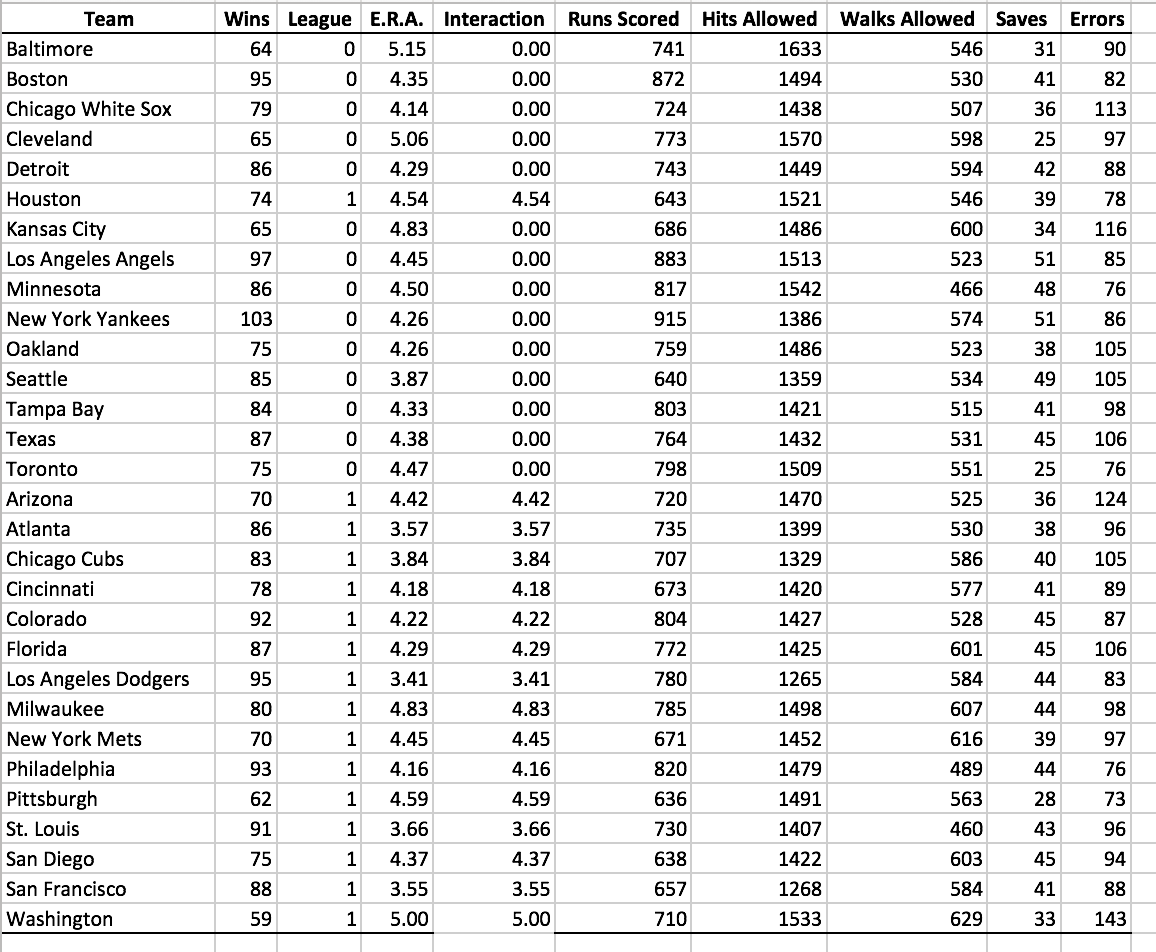
2. A baseball analytics specialist wants to determine which variables are important in predicting a team's wins in a given season. He has collected data related to wins, earned run average (ERA), and runs scored per game for a recent season (stored in Baseball.xlsx) (attached pic). Develop a model to predict the number of wins based on ERA and runs scored per game.

a. State the multiple regression equation and interpret the meaning of the slopes in this equation.

b. Is there a significant relationship between the number of wins and the two independent variables (ERA and runs scored per game) at the 0.05 level of significance? Explain.

c. At the 0.05 level of significance, determine whether each independent variable makes a significant contribution to the regression model. Explain.

d. Construct a 95% confidence interval estimate of the population slope between wins and ERA.

Suppose the analytics specialist decides to drop runs scored per game and to include the league (0 = American, 1 = National) as an independent variable in addition to ERA. Develop a model to predict wins based on ERA and league. For (e) through (g), DO NOT include an interaction term.

e. State the multiple regression equation and interpret the meaning of the slopes in this equation.

f. Is there a significant relationship between the number of wins and the two independent variables (ERA and league) at the 0.05 level of significance? Explain.

g. At the 0.05 level of significance, determine whether each independent variable makes a significant contribution to the regression model. Explain.

h. Add an interaction term to the model and at the 0.05 level of significance, determine whether it makes a significant contribution to the model.

Movie Tomatometer Rating Receipts The Mummy 16 7.8 Zookeeper's Wife 61 6.1 Beatriz at Dinner 80 28.4 The Hero 76 11.3 Wonder Woman 93 24.8 Baby Boss 52 13.3 The Circle 15 2.9 Dean 61 4 Baywatch 20 5.1 Churchill 38 1.9Team Wins League E.R.A. Interaction Runs Scored Hits Allowed Walks Allowed Saves Errors Baltimore 64 0 5.15 0.00 741 1633 546 31 90 Boston 95 0 4.35 0.00 872 1494 530 41 82 Chicago White Sox 79 0 4.14 0.00 724 1438 507 36 113 Cleveland 65 0 5.06 0.00 773 1570 598 25 97 Detroit 86 0 4.29 0.00 743 1449 594 42 88 Houston 74 4.54 4.54 643 1521 546 39 78 Kansas City 65 0 4.83 0.00 686 1486 600 34 116 Los Angeles Angels 97 0 4.45 0.00 883 1513 523 51 85 Minnesota 86 0 4.50 0.00 817 1542 466 48 76 New York Yankees 103 O 4.26 0.00 915 1386 574 51 86 Oakland 75 0 4.26 0.00 759 1486 523 38 105 Seattle 85 0 3.87 0.00 1359 534 49 105 Tampa Bay 84 0 4.33 0.00 803 1421 515 41 98 Texas 87 0 4.38 0.00 764 1432 531 45 106 Toronto 75 O 4.47 0.00 798 1509 25 76 Arizona 70 4.42 4.42 720 1470 525 36 124 Atlanta 86 3.57 3.57 735 1399 530 38 96 Chicago Cubs 83 P 3.84 3.84 707 1329 586 40 105 Cincinnati 78 4.18 4.18 673 1420 577 41 89 Colorado 92 4.22 4.22 804 1427 528 45 87 Florida 87 H 4.29 4.29 772 1425 601 45 106 Los Angeles Dodgers 95 3.41 3.41 780 1265 584 44 83 Milwaukee 80 4.83 4.83 785 1498 607 44 98 New York Mets 70 1 4.45 4.45 1452 616 39 97 Philadelphia 93 4.16 4.16 820 1479 489 44 76 Pittsburgh 62 1 4.59 4.59 636 1491 563 28 73 St. Louis 91 1 3.66 3.66 730 1407 460 43 96 San Diego 75 4.37 4.37 1422 603 45 94 San Francisco 88 3.55 3.55 657 1268 584 41 88 Washington 59 1 5.00 5.00 710 1533 629 33 143