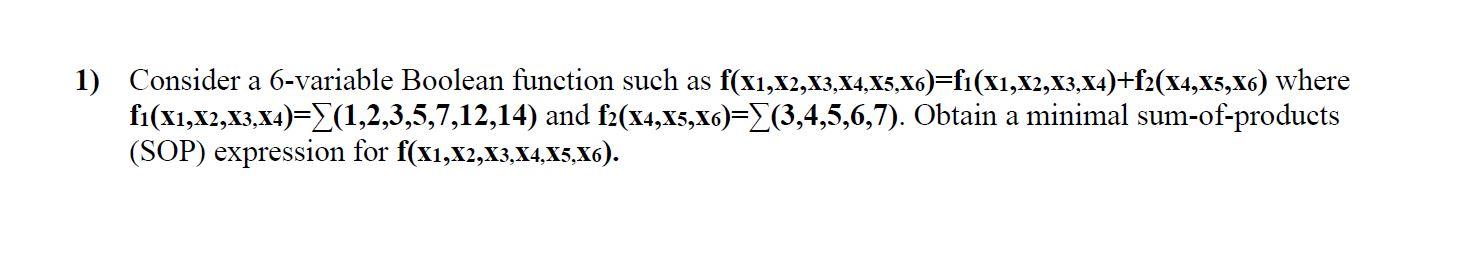Question: 1) Consider a 6-variable Boolean function such as f(x1,x2,x3,x4,x5,x6)=f1(x1,x2,x3,x4)+f2(x4,x5,x6) where f1(x1,x2,x3,x4)=(1,2,3,5,7,12,14) and f2(x4,x5,x6)=(3,4,5,6,7). Obtain a minimal sum-of-products (SOP) expression for f(x1,x2,x3,x4,x5,x6).

1) Consider a 6-variable Boolean function such as f(x1,x2,x3,x4,x5,x6)=f1(x1,x2,x3,x4)+f2(x4,x5,x6) where f1(x1,x2,x3,x4)=Σ(1,2,3,5,7,12,14) and f2(x4,x5,x6)=Σ(3,4,5,6,7). Obtain a minimal sum-of-products (SOP) expression for f(x1,x2,x3,x4,x5,x6).

1) Consider a 6-variable Boolean function such as f(x1,x2,x3,x4,x5,x6)=f1(x1,x2,x3,x4)+f2(x4,x5,x6) where f1(x1,x2,x3,x4)=Σ(1,2,3,5,7,12,14) and

Step by Step Solution

★★★★★

3.41 Rating (157 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

tq1 A3 93 74 Em ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Computer Engineering Questions!

x1 - 3x2 + x3 = 4 2x1 - x2 = - 2 4x1 - 3x3 = 0 Solve by Cramer's rule, where it applies.

Consider the MPS record below Wk 1 2 3 4 5 6 Forecast 15 25 9 15 22 5 Orders 7 10 10 10 Available ATP MPS On hand = 5, Lot size = 30 a. Complete the MPS record b. Update the record from part a -...

Consider two forces F1 = {10, 0} and F2 = 5{cos , sin }. (a) Find F1 + F2 as a function of . (b) Use a graphing utility to graph the function in part (a) for 0

Consider the sensitivity report below for problems 1-4. 1. Which of the following constraints are binding? Packing only Additive only Extrusion and Packaging Extrusion only All constraints are...

How do I use solver to find the decision variables and the constraints in the model section? 3 Data 10 11 12 13 14 15 16 17 18 Model 19 20 21 2.2 23 24 25 25 27 29 30 Math Formulation 31 33 34 35 36...

The Bayside Art Gallery is considering installing a video camera security system to reduce its insurance premiums. A diagram of Bayside's eight exhibition rooms is shown in figure below; the openings...

Consider the spreadsheet for Stone Age Surfboards provided below. Use this data to answer the following question(s), using the Standard Solver. Stone Age Surfboards is a small manufacturer of two...

[Chapter 12] Integer Linear Optimization Models Sunrise Investment Group is considering investing in six new projects. The require capital at the present time and the expected net present value (NPV)...

Fairland Marketing Group is a full-service marketing research company. Fairland is being hired to interview registered voters in a district to gain insights into their opinions about certain issues....

Garden City Beach is a popular summer vacation destination for thousands of people. Each summer, the city hires temporary lifeguards to ensure the safety of the vacationing public. Garden City's...

In this exercise, we will look at sorting in Prolog. a. Write Prolog clauses that define the predicate sorted (L), which is true if and only if list L is sorted in ascending order. b. Write a Prolog...

During the examination of the financial records of various company clients you find the following material items: (a) (b) (c) The profit and loss account of Freddy's Conner Ltd for the year ended 30...

L'Hopitals Rule Which function grows faster: f ( x ) = x 1 0 0 or g ( x ) = e x ? Consider the lim x x 1 0 0 e x to make your decision. Explain your reasoning.

Briefly write the characteristics of a conservative force give two examples n

Q4. Which of the following is a conservative force? (A) = yt-x} (B) F = yxt - xy) (C) F = yt + x) (D) F = yxt + xy)

Q-3. For a particle with constant kinetic energy, which of the following quantities must also be constant? (A) Position (B) Speed (C) Velocity (D) Momentum

Q-2. Which way does - point for the earth? (A) Parallel to NS axis and pointing north (B) Parallel to NS axis and pointing south (C) Parallel to NS axis and pointing east (D) Parallel to NS axis and...

Q-1. The kinetic energy of A particle of mass m is moving with constant speed along a circular path of radius r its kinetic energy is (A)T = mr*62 (B) T =mr*w? (C)T =lw? (D) All correct

so explain, when you would use (-1)^n, (-1)^n+1, and (-1)^n-1

Consider the example of cleaning your dorm except now there are BOTH rewards and costs. Suppose you have , preferences with = 0.7 and = 1. You have to clean your room at some point over the next...

Multiple Choice Question 1. Consider the following information: ending inventory , $24,000; sales, $250,000; beginning inventory, $20,000; selling and administrative expenses, $70,000; and purchases,...

Suppose X1,...,Xk are independent, with Xi N(i, 1). Consider testing the null hypothesis 1 = = k = 0 against max |i| , for some > 0. Find a maximin level test as explicitly as possible. Compare...

1. Consider the matrix defined below. What value is referenced with ? (a) 7 (b) 10 (c) 5 (d) 3 (e) None of the above. 2. Consider the matrix defined below. What value is produced by the command ? (a)...

1. Consider the following two interest options for an investment of $1000: (A) 4% simple interest, (B) 3% interest compounded annually. After how many years will option B outperform option A? 2....

1. Consider a multiproduct company and discuss the likely sequence in which the average customer would buy these products. Why do you think an average customer may not be the best way to consider...