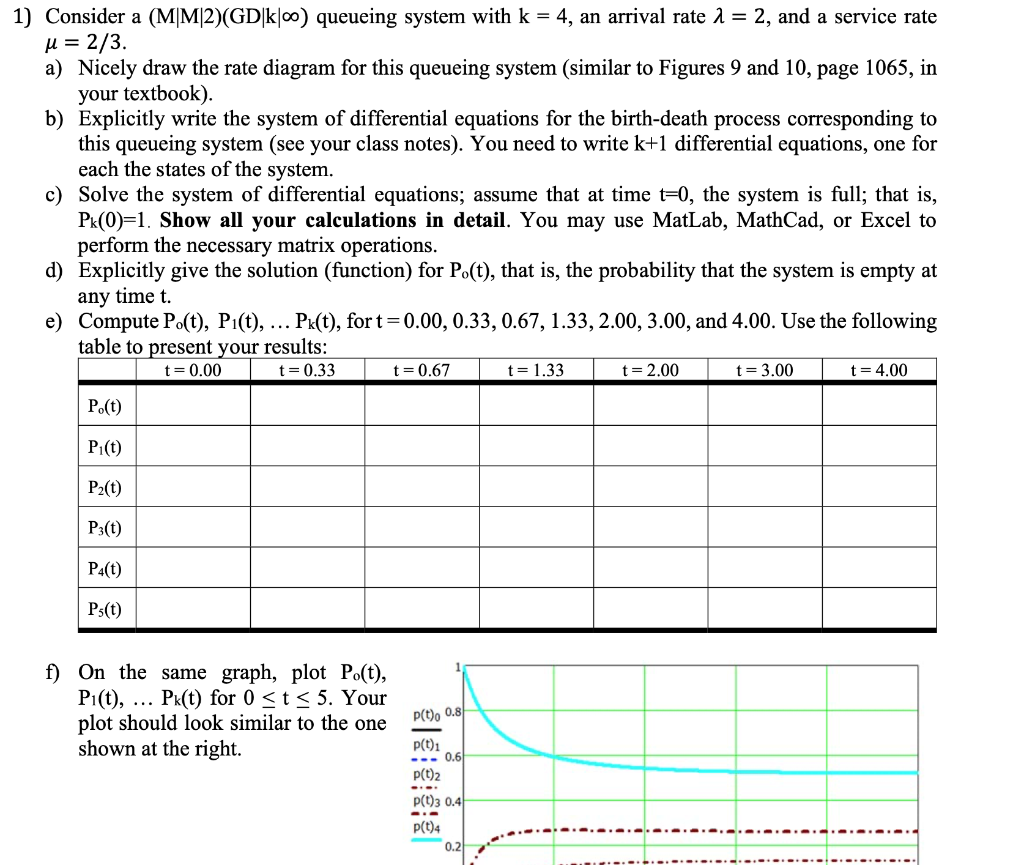
1) Consider a (M|M|2)(GD|k|) queueing system with k = 4, an arrival rate = 2, and a service rate = 2/3. a) Nicely draw the rate diagram for this queueing system (similar to Figures 9 and 10, page 1065, in your textbook). b) Explicitly write the system of differential equations for the birth-death process corresponding to this queueing system (see your class notes). You need to write k+1 differential equations, one for each the states of the system. c) Solve the system of differential equations; assume that at time t=0, the system is full; that is, Pk(0) 1. Show all your calculations in detail. You may use MatLab, MathCad, or Excel to perform the necessary matrix operations. d) Explicitly give the solution (function) for Po(t), that is, the probability that the system is empty at any time t. e) Compute Po(t), P1(t), ... Pk(t), for t=0.00, 0.33, 0.67, 1.33, 2.00, 3.00, and 4.00. Use the following table to present your results: Po(t) Pi(t) P2(t) P3(t) P4(t) Ps(t) t=0.00 t=0.33 f) On the same graph, plot Po(t), Pi(t), ... Pk(t) for 0 t 5. Your plot should look similar to the one shown at the right. t=0.67 t = 1.33 t=2.00 P(t) 0.8 p(t)1 -0.6 p(t)2 p(t)3 0.4 -- p(t)4 0.2 t=3.00 t=4.00