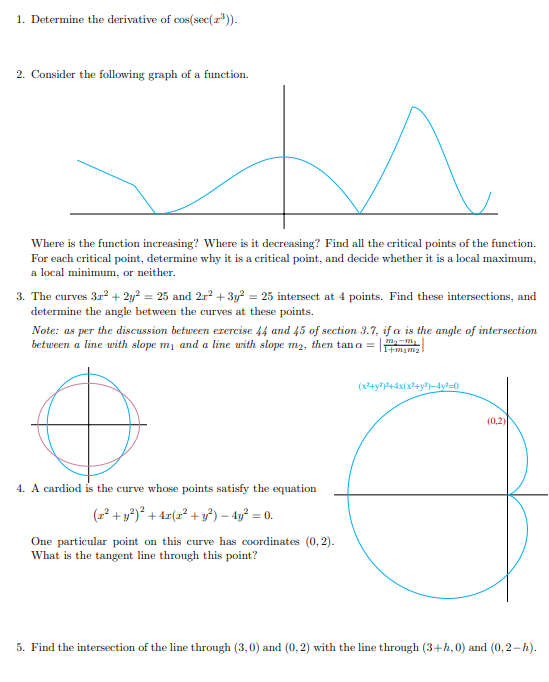
1. Consider the function f(x) = 5x3 + 3x + x + . (a) Find all of the inflection points of f. (b) For what values of is the inflection point also a critical point? Is it a local maximum, a local minimum, or neither? (c) Sketch the curve for this value of , assuming you also know that f(-1) = 0. (d) For what values of does the function have two critical points? Classify the critical points, in this situation. (e) Sketch the curve when both a and are equal to zero. 2. Sketch the curve y = f(x)= = (x+4)(x-3) (x-2)(x+3) 3. Sketch the curve y = f(x) = = (x+3)(x-3) (x-2)(x+4)* Note that this differs from the curve in 2 by swapping one of the factors in the numerator with one of the factors in the denominator. Compare the result with your sketch in 2. 1. Find the maximum and minimum values of 40-||-413-37| when 0x6, if they exist. 2. Find all of the critical points of f(x) = sin x-sin x on 0x, and classify them according to whether they are local maxima, local minima, or neither. 3. Find the maximum possible volume of a conical paper cup that can be produced by 'folding' a circle of radius 4 so that a sector of central angle overlaps itself. 4. Use Newton-Raphson iterations to solve tan(x) = 1. 1. Determine the derivative of cos(sec(z)). 2. Consider the following graph of a function. Where is the function increasing? Where is it decreasing? Find all the critical points of the function. For each critical point, determine why it is a critical point, and decide whether it is a local maximum, a local minimum, or neither. 3. The curves 3x + 2y = 25 and 2x + 3y = 25 intersect at 4 points. Find these intersections, and determine the angle between the curves at these points. Note: as per the discussion between exercise 44 and 45 of section 3.7, if a is the angle of intersection between a line with slope m and a line with slope m2, then tana = m-m 1+mim2 4. A cardiod is the curve whose points satisfy the equation (x + y) + 4x(x + y) 4y = 0. One particular point on this curve has coordinates (0,2). What is the tangent line through this point? (x+y2)+4x(x+y2)4y=0 (0,2) 5. Find the intersection of the line through (3,0) and (0,2) with the line through (3+h, 0) and (0,2-h).