Question
1) Define the degree of a vertex of an undirected graph as the number of edges incident on that vertex. Prove that an undirected graph
1) Define the degree of a vertex of an undirected graph as the number of edges incident on that vertex. Prove that an undirected graph must have an even number of vertices of odd degree.
2) Fill out the table below to show how to traverse this graph using BFS. Your start node is A. When you have a choice of the next node to process, choose the one earliest in the alphabet. In terms of the queue, the first element should be in the Node @ Head column, the order of the other nodes on the queue doesnt matter.
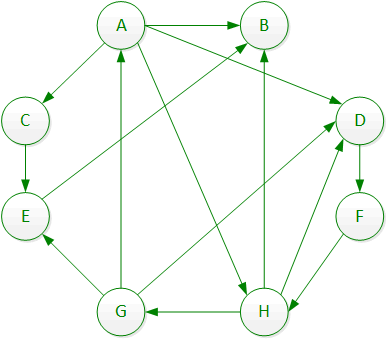
| . Node | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| (init) |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Step by Step Solution
There are 3 Steps involved in it
Step: 1
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2
Step: 3
Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started
Big Data Concepts, Theories, And Applications
Authors: Shui Yu, Song Guo
1st Edition
3319277634, 9783319277639
