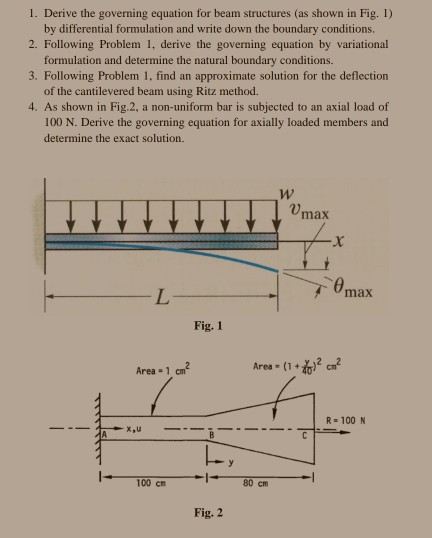
1. Derive the governing equation for beam structures (as shown in Fig. 1) by differential formulation and write down the boundary conditions. 2. Following Problem 1, derive the governing equation by variational formulation and determine the natural boundary conditions. 3. Following Problem 1, find an approximate solution for the deflection of the cantilevered beam using Ritz method. 4. As shown in Fig.2, a non-uniform bar is subjected to an axial load of 100 N. Derive the governing equation for axially loaded members and determine the exact solution. L Area - 1 cm mory X,U 100 cm Fig. 1 Fig. 2 W 80 cm Vmax Area - (1+ cm max R = 100 N