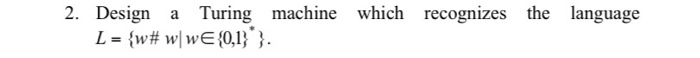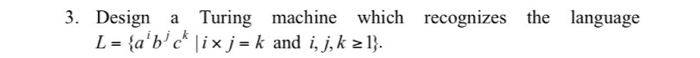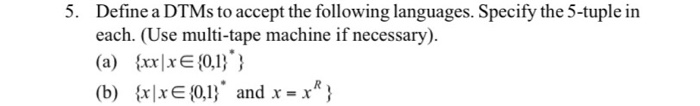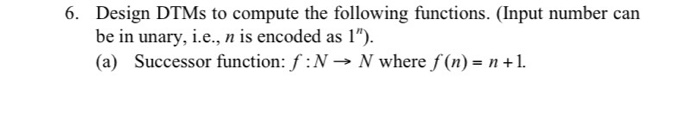1. Design a Turing machine which recognizes the language consisting of all strings of Os whose length is a power of 2. i.e., it decides the language L = {0?" | n 20;. recognizes the language 2. Design a Turing machine which L = {w# w WE{0,1}}. recognizes the language 3. Design a Turing machine which L = {a'biclix j = k and i, j, k 21}. 4. Design a deterministic Turing machine (DTM) to accept the language L = {a'b'ci 20%. Define a DTMs to accept the following languages. Specify the 5-tuple in each. (Use multi-tape machine if necessary). (a) {xx|x {0,1}} (b) {x|x {0,17" and x = rp} 6. Design DTMs to compute the following functions. (Input number can be in unary, i.e., n is encoded as 1"). (a) Successor function: f:N N where f(n)= n +1. (b) f:N ~ N N such that f(a,b) = (a/b] (c) f:N N such that f(n) = [log, nl. 7. Define Nondeterministic Turing machines to accept the following languages. (a) {xx|x {0,1}" } (b) XXE {0,13* and x = x 8. Define a multiheaded Turing machine, a model in which each tape can have k tape heads. Prove that a Deterministic Turing Machine (DTM) with one work tape can simulate a two-headed Turing machine. 9. Design a Turing machine which computes the function f(n,n) = min(ni, n,) for all non-negative integers n, and n. 10. Design a Turing machine which computes the function f(n) = 3 if n 25 and f (n) = 0 if n=0, 1, 2, 3 or 4. 11. Construct a Turing machine which computes the function f(n)=n mod 12. Design a Turing machine which recognizes the set {0"1"2"|n 20). 13. Design a TM that recognizes the set of all bit strings that contain an even number of 19 14. Construct a TM that recognizes the set of all bit strings which end with a 15. Design a Turing machine with tape symbols 0, 1 and B that given a bit string as input, replaces all but the leftmost I on the tape with Os and does not change any of the other symbols on the tape. 16. Design a TM with tape symbols 0, 1 and B that replaces the first O with a 1 and does not change any of the other symbols on the tape. 17. Design a TM that recognizes the set {02"1" |n 20; 18. Show that the recursiveness problem of Type-0 grammars is unsolvable. 19. Show that the problem of determining whether or not a TM over {0,1} will print ever the symbol 1, with a given tape configuration is unsolvable. 20. Show that there exists a TM for which the halting problem is unsolvable