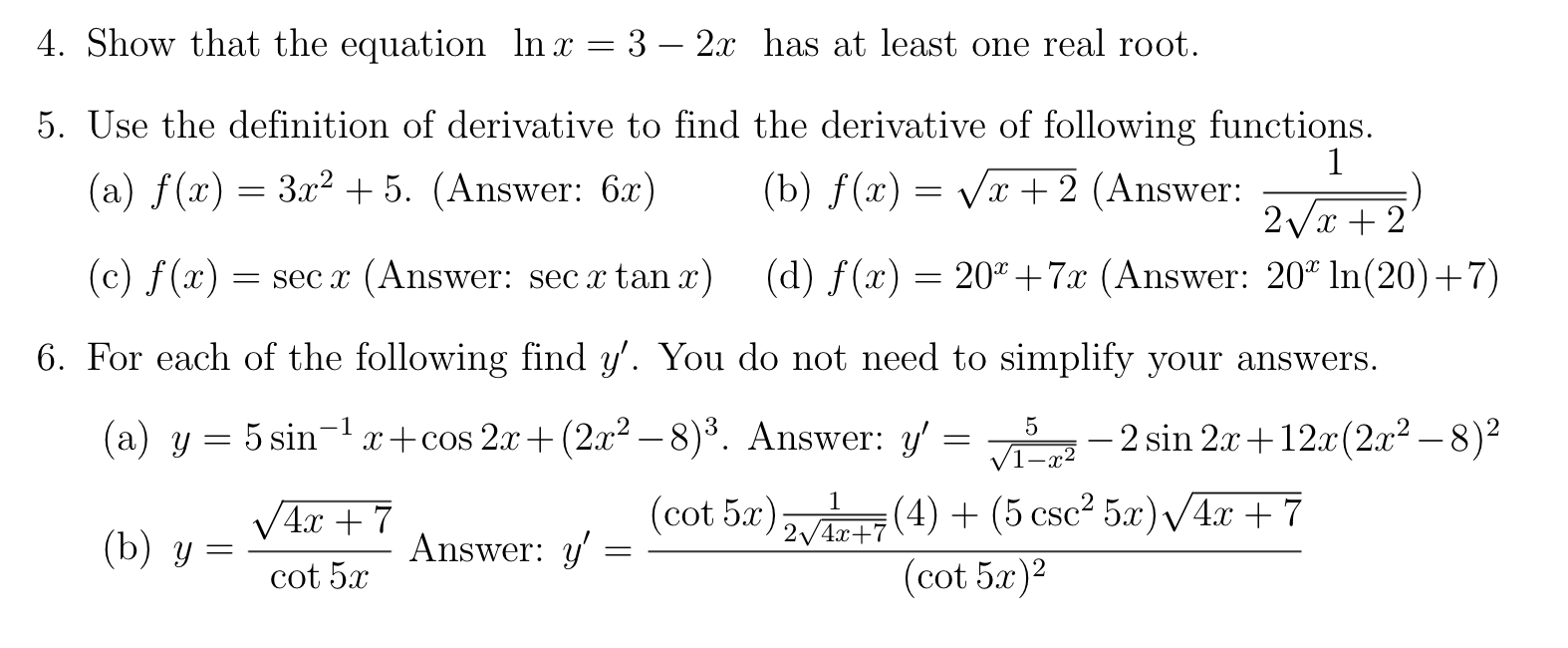
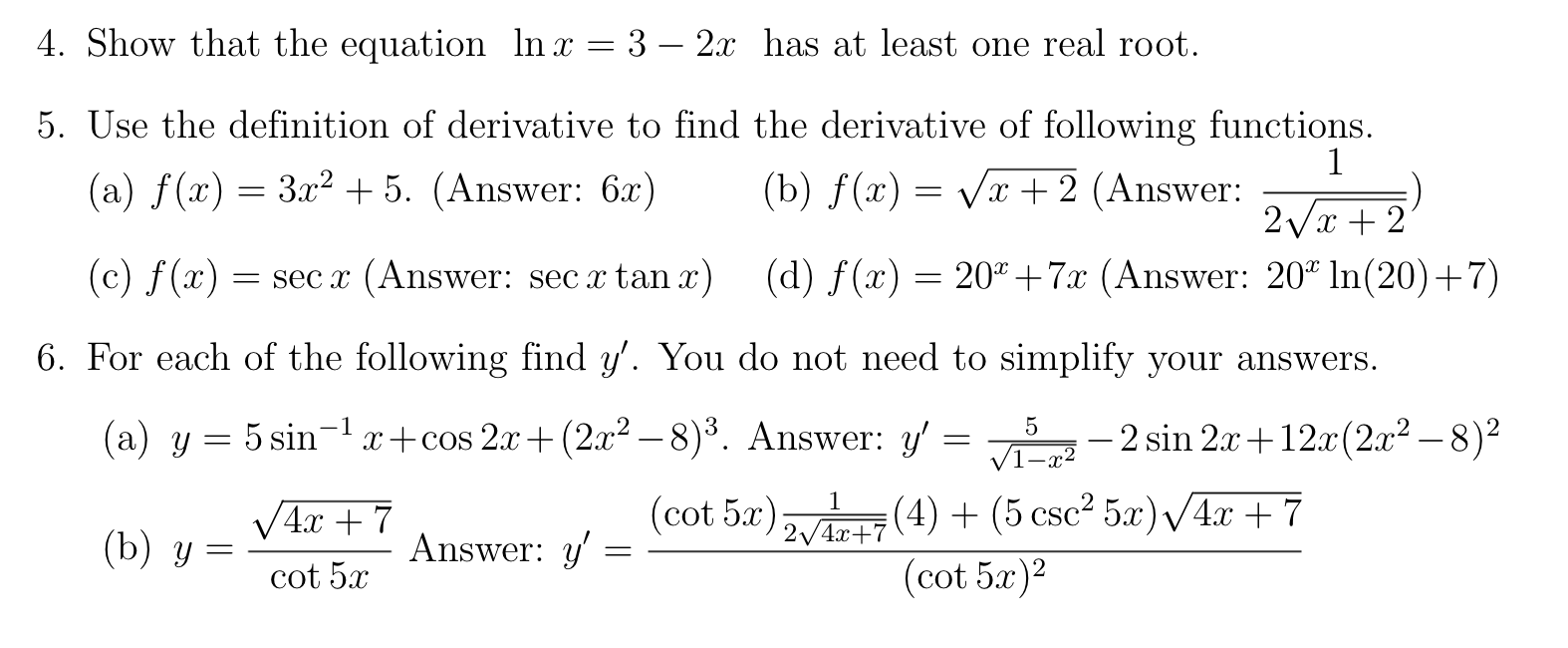
1. Evaluate the following limits if they exist. 3x2 - 6x + 8 (a lim x-70 2 - 4x + 7 (Do not use L'Hospitals Rule) Answer: 3 (b) lim 2 2 - 8x + 12 2-2 202 - 3x + 2 (Do not use L'Hospitals Rule) Answer: -4 (c) lim In x tan(7x/2). Answer: - d) lim x cos Answer: 0 x-+0 525 (e lim (2 - 51 5 Answer: LHLX RHL, the limit DNE x-5 (f) lim a . Answer: 1 g) lim x - 1 x-+ 1 Vac - 1 (Do not use L'Hospitals Rule) Answer: 2 (h) lim tan x - X Answer: ? x-0 (i) lim (cos x ) 1/ 22 a. Answer: 1/ Ve (j) lim vax sin - Answer: 0 5x 2. Find all the horizontal and vertical asymptotes of the curve y = 202 - 3x + 2 x2 - 4x + 3 Answer: x = 3, y = 1. 3. Show that the function is continuous on R. f (20 ) = Ja sin(1/x), if x * 0 10, if x = 04. Show that the equation In x = 3 - 2x has at least one real root. 5. Use the definition of derivative to find the derivative of following functions. 1 (a) f(x) = 3x2 + 5. (Answer: 6x) (b) f(ac) = vx+2 (Answer: 2Vx + 2 (c) f(x) = sec x (Answer: sec x tan x) (d) f(x) = 20* +7x (Answer: 20% In(20) +7) 6. For each of the following find y'. You do not need to simplify your answers. (a y = 5 sin x + cos 2x + (2x2 -8)3. Answer: y' = 5 V1-72 - 2 sin 2x + 12x(2x2 -8)2 V 4x + 7 (cot 5x) 1 2V4x+7 (4) + (5 csc2 520) V 4x + 7 ( b) y = Answer: y' = cot 5x (cot 5x)210. 11. 12. 13. . Find the values of CE where the tangent line to the curve y = tan' (0) y 2 63! + sec :13. Answer: y' = 8313' ' 35':3 - ln3 - 3x2 + seczctansv 33inzr: (d) y = (1 + 3503"". Answer: y' 2 (1+ 310511190 1 + 3:1; + cosa: ln(1 + 33:) 23:y 2 .2 l 3?.) +1 _ 1er2 (9) 313 + 1162?; = tan*1 y Answer: y' = (f) y = log(:c2 + 1). Answer: 3;" = W emy :r8y3 (g) 3131 + 7 2 6m + 23f. Answer: 9" : . Find the equation of tangent line to the curve 1'2 31y + y2 : 3 at point (1.1). Answer: y = x + 2 . For what values of a: in [0, 2w] does the graph of f (1:) : ZL' | 2 sing: have a horizontal 27T 47F tangent? Answer: :3 = E or :10 = 3 11: is parallel to the line y = 53/5 + 2. Answer: a: = 2, 2 Find the absolute minimum and absolute maximum values of x) : :31: on the interval [4.4]. Answer: Abs. Max.= f(4) = f(4) = 0.6, Abs. Min.=f(0) = 1 Find the absolute minimum and absolute maximum values of f (:L) : 1* + cot(:;r: / 2) on the interval [Tr/4, 77T/4]. Answer: f(7r/2) = 7r/2 + 1, f(37T/2) = 37r/2 1 Verify that the function f (:13) = :53 +56 1 satisfies the hypotheses of the Mean Value Theorem on the interval [0, 2]. Then find all numbers 0 that satisfy the conclusion of the Mean Value Theorem. Answer: c : 2/ \/ Let f(:1;) : [ac3)". Show that there is no number a in (1, 4) such that f(4) f(1) = f' (c) (4 1). Why does this not contradict the Mean Value Theorem. 14. Using 331 = 1, perform two iterations of Newton's method (calculate 1'3) to estimate the solution to the equation 3:3 + 23: : 4. Answer: 2:2 : 1.2, :33 : 1.1797468 15. (a) Use the intermediate value theorem to show that the equation 305 = 1 213 has at least one real root. (b) Use Rolle's theorem to show that the equation 305 = 1 2:1; has at most one real root. (c) Using :L'1 = 0, perform two iterations of Newton's method (calculate 333) to estimate the solution to the equation 2:5 : 12.",6. Answer: $2 = 0.5, 333 = 0.4865 16. Approximate the value of 111 1.01 using linear approximation. Answer: 0.01 17. Car A is travelling west at 50 mi / h and car B is travelling north at 60 mi / h. Both are headed for the intersection of the two roads. At what rate are the cars approaching each other when car A is 0.3 mi and car B is 0.4 mi from the intersection? Answer: 78 mi/h. 18. 19. 20. 21. 22. 23. A kite 100ft above the ground moves horizontally at a speed of 8 ft/s. At what rat is the angle between the string and the horizontal decreasing when 200 ft of strin has been let out? Answer: 0.02 rad/s A rectangular storage container with an open top is to have a volume of 10m3. Th length of its base is twice the width. Material for the base costs $10 per squar meter. Material for the sides costs $6 per square meter. Find the cost of material for the cheapest such container. Answer: $163.54 (a) Find the most general antiderivative of ac) 2 2M3 -| 6 cos :3. Answer: g '3/2 + 63inx | C (b) Find the most general antiderivative of f($) : VH6 -l 51'). Answer: 4333/2 + 2:1:5/2 + C Let A be the area of the region that lies under the graph of f(1:) = 23:2 + 5 betwee: :1: : 0 and r = 4. Using right endpoints find expressions for A as a limit. Evaluat the limit without using the Fundamental Theorem of Calculus. n n 1 2f 1 (Recall that 21 = n and :22 = W) Answer: % Let A be the area of the region that lies under the graph of f($) = 2:133 betwee: :1: = 0 and $ = 3. Find an expression for the area A as a limit. Evaluate the limi without using the Fundamental Theorem of Calculus. n n(n | 1) 2 , Recall that :23 = (2) Answer: 8721 i=1 7 Evaluate the integral / V 49 3:2 dac by interpreting it in terms of area. 17 49 Answer: 77? 24. For each of the functions (i) f(x) = 25/3 - 5x2/3 (ii) f (ac ) = 2 2 - 1 (a) State the domain of f. (b) Find the x and y intercepts. (c) Does f have even symmetry, odd symmetry, or neither? (d) Determine the vertical asymptote(s) of the curve y = f(x) (if any), and deter- mine the left and right limits at each of these asymptotes. (e) Determine the horizontal asymptote(s) of the curve y = f(x) (if any). (f) Find the intervals of increase / decrease. (g) Determine the points at which f has a local maximum/local minimum. (h) Find the intervals of concavity. (i) Determine the inflection points. (j) Sketch the graph y = f(x) using above information