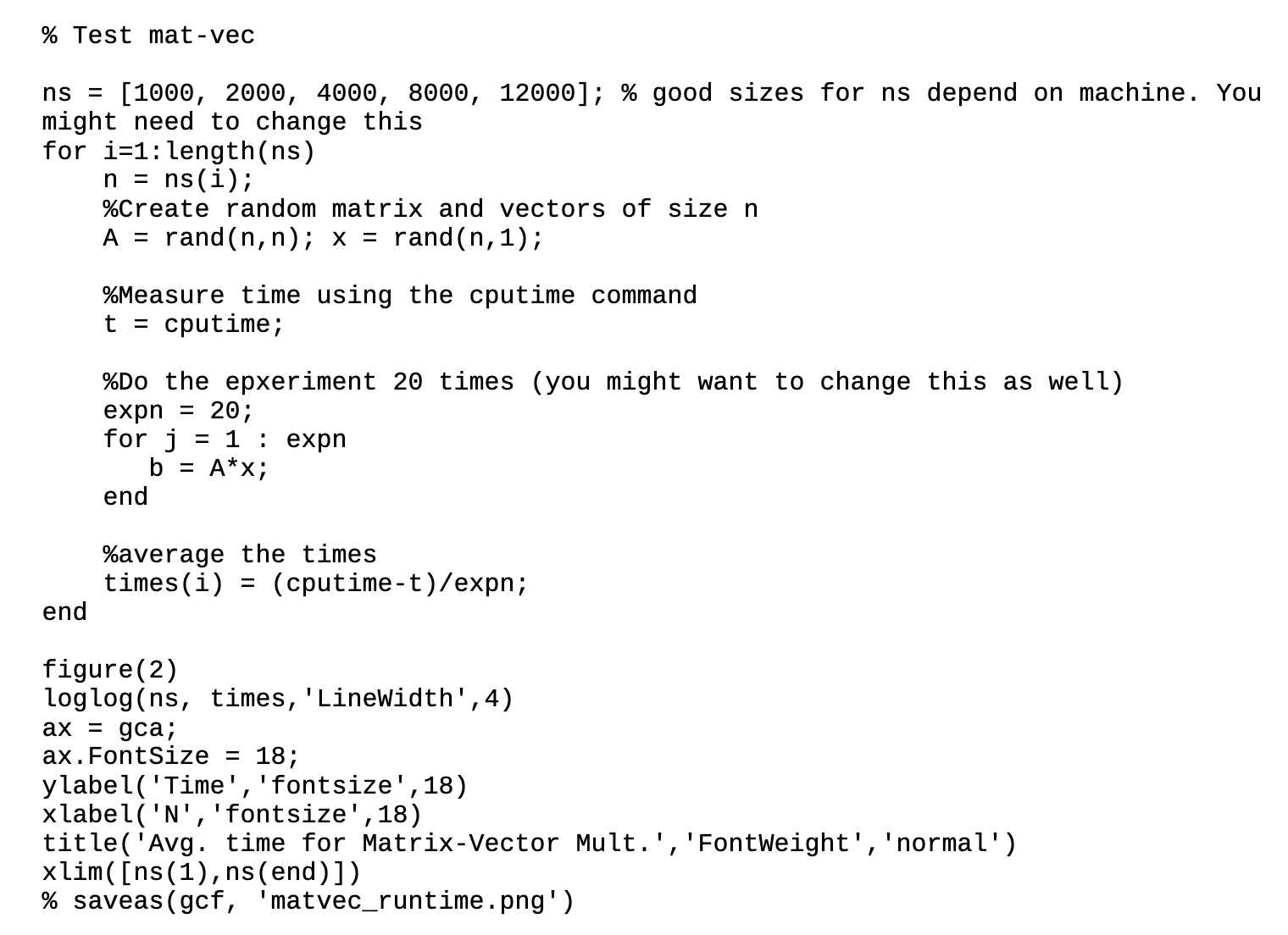
1. FLOPS On the course Canvas page (attached to this homework assignment), you will find a script test flops.m that generates a plot for the run-time of a mat-vec operation over different problem sizes. 1 (a) Modify this file in order to plot a similar timing graph for matrix-matrix multi- plication. Make sure to use appropriate axis scaling and readable labels. Use the Matlab command A * B to perform the matrix-matrix multiply where A, B are n x n matrices. Find the exhibited big-Oh notation for the runtime, e.g., O(n), O(n), O(n),... Justify your answer from your plot. (b) Repeat the previous problem, but now instead of a single matrix operation (A + B), consider multiple Mat-Mat operations. Time the cost of the calculation A * B + C * D for n n matrices A, B, C, and D and generate the relevant plot. Does the operation still have the same big-Oh runtime as in part (a)? Explain. % Test mat-vec ns = [1000, 2000, 4000, 8000, 12000]; % good sizes for ns depend on machine. You might need to change this for i=1:length(ns) end n = ns(i); %Create random matrix and vectors of size n A = rand(n,n); x = rand(n, 1); % Measure time using the cputime command t = cputime; %Do the epxeriment 20 times (you might want to change this as well) expn = 20; for j = 1 expn end b = A*x; %average the times times(i) = (cputime-t)/expn; figure(2) loglog(ns, times, 'LineWidth', 4) ax = gca; ax. FontSize = 18; ylabel('Time', 'fontsize',18) xlabel('N', 'fontsize', 18) title('Avg. time for Matrix-Vector Mult.', 'FontWeight', 'normal') xlim([ns(1), ns (end)]) % saveas (gcf, 'matvec_runtime.png') 2. Numerical Invertibility (a) Show that the matrix 1 4 A=258 -23 6 9 is singular. Find a vector in the null-space of A (i.e. a nonzero vector such that Ay = 0). Does the equation Ax = b have no solutions, one solution, or infinitely many solutions if 1 b = 3? 5 (b) Solve the linear system Ax = b in MATLAB with backslash. Does MATLAB think the matrix is singular? If not, describe why. (c) Now define a new problem x = where = 1 10 1 A, = -b. 10 This problem should have the same solution x. If you were to try to solve this problem by hand, you would encounter the same issue as part (b). Try to solve this problem in MATLAB using the backslash command. Does MATLAB think the matrix is singular? If not, describe why. 3. Linear Algebra Exercises (a) Prove that if L is lower-triangular and invertible, then the matrix A = L- is also lower triangular. 2 (b) A square matrix is symmetric if transposing it (or reflecting the entries across the diagonal) doesn't change the matrix. Put another way, A is symmetric if the entries obey aij = aji. Prove the following statement, or find a counter- example: if A and B are both symmetric, then C = AB is also symmetric. 4. Matrix Inversion Consider the system of equations x+2yz = 10, 2xy + z = 3, 3x-2y+2z = 3. (a) Solve this system by hand using techniques from high-school algebra and keep track of the "flops" required (anytime you multiply, add, subtract, or divide two numbers). (b) Now reform the problem as a matrix equation Ax = b. (c) Calculate the inverse matrix A-1 and perform the multiplication A-6. Count the number of flops required and compare with part a).