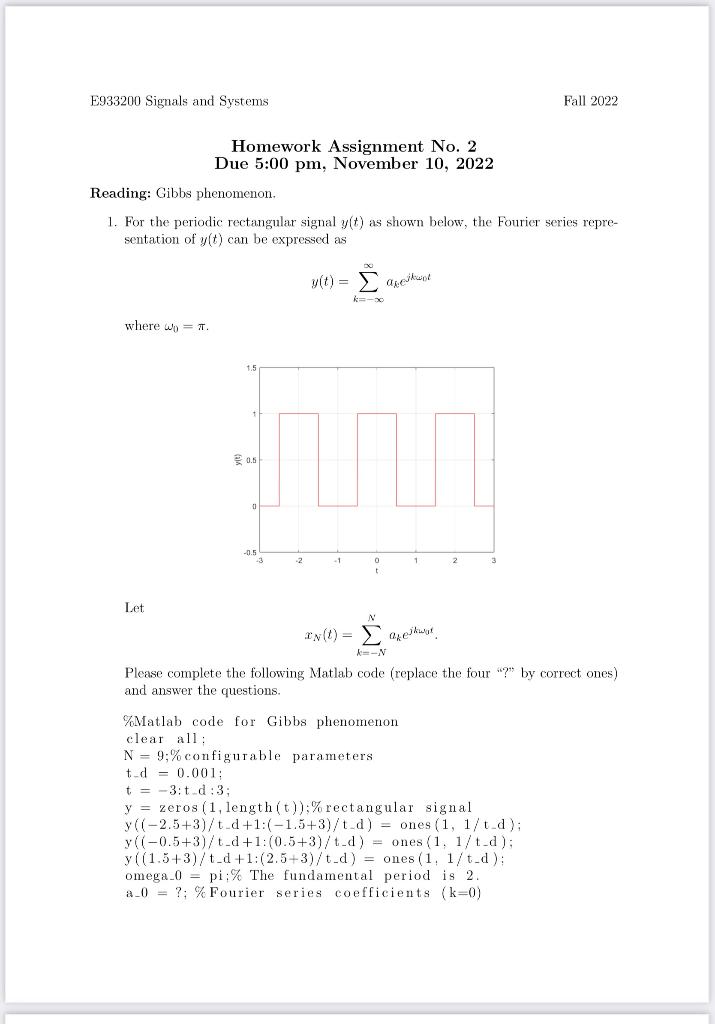

1. For the periodic rectangular signal y(t) as shown below, the Fourier series representation of y(t) can be expressed as y(t)=k=akejk0t where 0=. Let xN(t)=k=NNahejkt. Please complete the following Matlab code (replace the four "?" by correct ones) and answer the questions. \%Matlab code for Gibbs phenomenon clear all : N=9;% configurable parameters td=0.001; t=3:td:3; y= zeros(1, length(t));\%rectangular signal y((2.5+3)/t _d +1:(1.5+3)/t - d)= ones (1,1/t _d ); y((0.5+3)/td+1:(0.5+3)/td)= ones (1,1/td) y((1.5+3)/td+1:(2.5+3)/t d )=ones(1,1/t d ) omega_0 = pi;\% The fundamental period is 2 . a_ 0=?;% Fourier series coefficients (k=0) (a) (10%) Find a0. (b) (10%) Find ak for k=0. (c) (10%) Find x1(0.3). (d) (10%) Also find x49(0.9). (e) (10%) Find x1(0),x3(0),x9(0),x99(0), and x999(0). (f) (10%) Find x1(0.5),x3(0.5),x9(0.5),x99(0.5), and x999(0.5). (g) (5%) Find the maximum value of x1(t) and tmax=argmax0t1x1(t). (h) (5%) Find the maximum value of x3(t) and tmax=argmax01x3(t). (i) (5\%) Find the maximum value of x5(t) and tmax=argmax0t1x5(t). (j) (5\%) Find the maximum value of x9(t) and tmax=argmax0t1x9(t). (k) (5%) Find the maximum value of x99(t) and tmax=argmax01x99(t). (1) (5\%) Find the maximum value of x9g9(t) and tmax=argmax0t1x999(t). (m) (10\%) Provide your observations according to the results of (e) to (1). 1. For the periodic rectangular signal y(t) as shown below, the Fourier series representation of y(t) can be expressed as y(t)=k=akejk0t where 0=. Let xN(t)=k=NNahejkt. Please complete the following Matlab code (replace the four "?" by correct ones) and answer the questions. \%Matlab code for Gibbs phenomenon clear all : N=9;% configurable parameters td=0.001; t=3:td:3; y= zeros(1, length(t));\%rectangular signal y((2.5+3)/t _d +1:(1.5+3)/t - d)= ones (1,1/t _d ); y((0.5+3)/td+1:(0.5+3)/td)= ones (1,1/td) y((1.5+3)/td+1:(2.5+3)/t d )=ones(1,1/t d ) omega_0 = pi;\% The fundamental period is 2 . a_ 0=?;% Fourier series coefficients (k=0) (a) (10%) Find a0. (b) (10%) Find ak for k=0. (c) (10%) Find x1(0.3). (d) (10%) Also find x49(0.9). (e) (10%) Find x1(0),x3(0),x9(0),x99(0), and x999(0). (f) (10%) Find x1(0.5),x3(0.5),x9(0.5),x99(0.5), and x999(0.5). (g) (5%) Find the maximum value of x1(t) and tmax=argmax0t1x1(t). (h) (5%) Find the maximum value of x3(t) and tmax=argmax01x3(t). (i) (5\%) Find the maximum value of x5(t) and tmax=argmax0t1x5(t). (j) (5\%) Find the maximum value of x9(t) and tmax=argmax0t1x9(t). (k) (5%) Find the maximum value of x99(t) and tmax=argmax01x99(t). (1) (5\%) Find the maximum value of x9g9(t) and tmax=argmax0t1x999(t). (m) (10\%) Provide your observations according to the results of (e) to (1)








