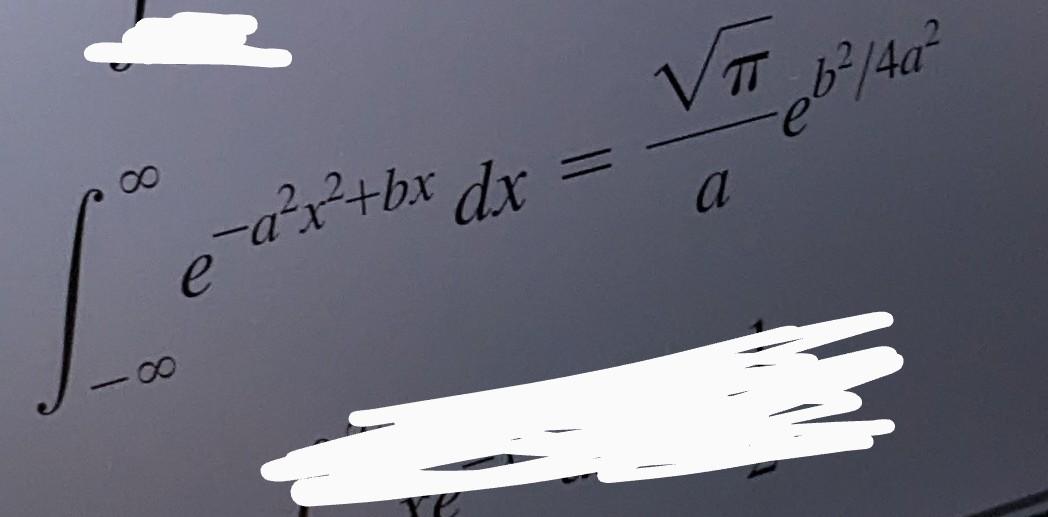
1. Free particles are often modeled as "wave packets". For example, we might start with an initial Gaussian wave function, (x, t = 0) = Aeax, with A and a both real and positive constants. a) Normalize (x, t = 0), and then calculate its momentum-space distribution: $(p,t = 0) = (x, t = 0); -ipx/hdx for this wave function. 2h Hints: If you are feeling ambitious, there's a trick to do integrals of the form fe-(ax+bx)dx, - b 4a' (This is called "completing the square: Let y = (x + b/2a) so that (ax + bx) = : = y valid even for complex b! What is "b" for your problem at hand?) Also note the handy Gaussian integral: e-cz dz = /c. b) Now calculate the time dependent wave function (x, t). The answer here is 4(x,t) = (2%) 1/4 1/4 e-ax/(1+int) (1+int) with 2ah/m (You will need to work out what is the dimensionless constant indicated by "?" above) c) Find the probability density |\/(x, t)|. Simplify your result by expressing it in terms of a new quantity defined as = 1+ (t). Then, find (x) and (p) as functions of time, and briefly discuss. d) Find (x2) and (p), and then Ax and Ap (all as functions of time). (If you need a computer to help, that's fine, just let the grader know.) Discuss the Heisenberg uncertainty principle for this problem. When is the system closest to the lower limit of AxAp? Helpful math hint: zec dz = /c. Another hint: For (p), you may find using the result from part a) makes it easier - work in momentum space.. 80 8 e-ax+bx dx = VT a e b/4a -