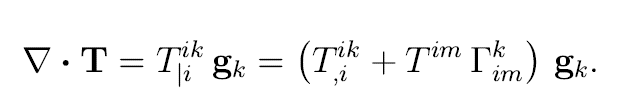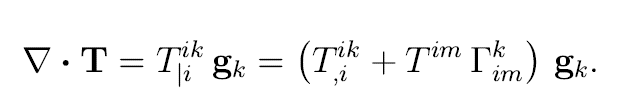
1. Given that the divergence of a Tensor Field

T=Tiikgk

Please verify if

\fThe Divergence of a Tensor Field Analogous to the definition 1.14.9, the divergence of a second order tensor T is defined to be the vector div T = grad T : 1 = of e, = ax, ax Divergence of a Tensor (1.14.12) = ax One also has V . Tze, ax, (1.14.13) ax so that divT = V. T (1.14.14) As with the gradient of a vector, both (87, / ax, Je, and (OT, / ax, )e, are commonly used as definitions of the divergence of a tensor. They are distinguished here by labelling theThe Christoffel Symbols of the Second Kind First, from Eqn. 1.16.19 - and using the inverse relation, a ax (1.18.1) this can be written as og, Partial Derivatives of Covariant Base Vectors (1.18.2) where (1.18.3) and I'd is called the Christoffel symbol of the second kind; it can be seen to be equivalent to the th contravariant component of the vector ag, /60. One then has { A Problem 1} og og g ao Christoffel Symbols of the 2nd kind (1.18.4) and the symmetry in the indices i and / is evident. Looking now at the derivatives of the contravariant base vectors g' : differentiating the relation g, g* =6, leads to Og* ag. L.q' = [ 8mg = DGeneralising Tensor Calculus from Cartesian to Curvilinear Coordinates It was seen in $1.16.7 how formulae could be generalised from the Cartesian system to the corresponding formulae in curvilinear coordinates. In addition, formulae for the gradient, divergence and curl of tensor fields may be generalised to curvilinear components simply by replacing the partial derivatives with the covariant derivatives. Thus: Cartesian Curvilinear Gradient Of a scalar field grado, Vo = ag/ ax, of a vector field gradu = du, / ax u'l, of a tensor field gradT = OT, /Oxx Divergence of a vector field divu, V . u = du, / ax, of a tensor field divT =OT, /ox, Curl of a vector field curlu, Vxu = &;x Qu , / ax, Table 1.18.1: generalising formulae from Cartesian to General Curvilinear Coordinates All the tensor identities derived for Cartesian bases ($1.6.9, $1.14.3) hold also for curvilinear coordinates, for example { _ Problem 11} grad(av ) = agradv + v @ grada div( vA) = v . divA + A : gradv