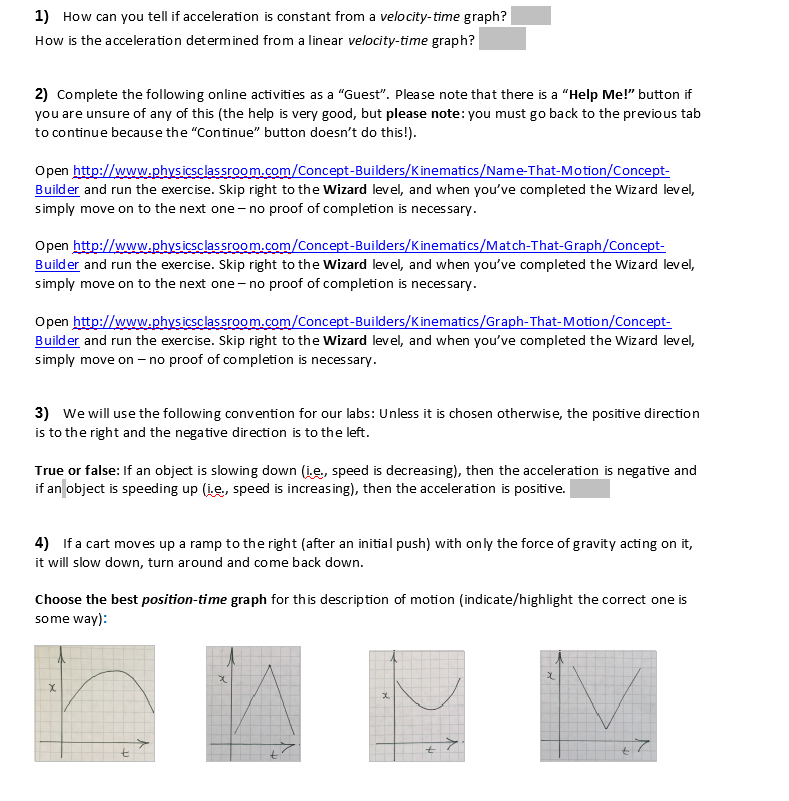
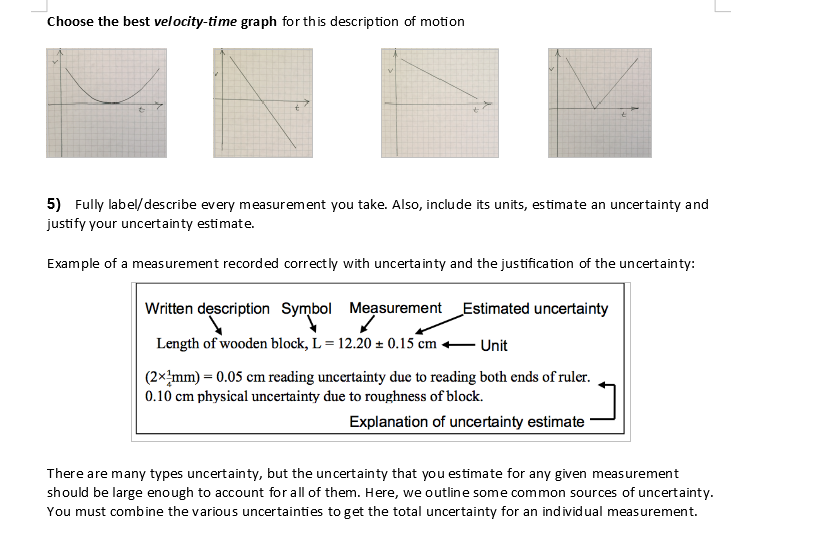
1) How can you tell if acceleration is constant from a velocity-time graph? How is the acceleration determined from a linear velocity-time graph? 2) Complete the following online activities as a "Guest". Please note that there is a "Help Me!" button if you are unsure of any of this (the help is very good, but please note: you must go back to the previous tab to continue because the "Continue" button doesn't do this!). Open http://www.physicsclassroom.com/Concept-Builders/Kinematics/Name-That-Motion/Concept- Builder and run the exercise. Skip right to the Wizard level, and when you've completed the Wizard level, simply move on to the next one - no proof of completion is necessary. Open http://www.physicsclassroom.com/Concept-Builders/Kinematics/Match-That-Graph/Concept- Builder and run the exercise. Skip right to the Wizard level, and when you've completed the Wizard level, simply move on to the next one - no proof of completion is necessary. Open http://www.physicsclassroom.com/Concept-Builders/Kinematics/Graph-That-Motion/Concept- Builder and run the exercise. Skip right to the Wizard level, and when you've completed the Wizard level, simply move on - no proof of completion is necessary. 3) We will use the following convention for our labs: Unless it is chosen otherwise, the positive direction is to the right and the negative direction is to the left. True or false: If an object is slowing down (ie., speed is decreasing), then the acceleration is negative and if an object is speeding up (ie., speed is increasing), then the acceleration is positive. 4) If a cart moves up a ramp to the right (after an initial push) with only the force of gravity acting on it, it will slow down, turn around and come back down. Choose the best position-time graph for this description of motion (indicate/highlight the correct one is some way): x x t x 7 8) For PHYS 1100 labs, you will be required to calculate the % uncertainty for all of your calculated results. To calculate uncertainties for your results, use the following rules: If 2 or more quantities are multiplied or divided, then the % uncertainty of the result is the sum of the % uncertainties of the values you are multiplying or dividing. It follows that squaring a value doubles its % uncertainty and taking the square root halves the % uncertainty. Multiplying or dividing a value by a constant does not change the % uncertainty of the result. Applying trig (or inverse trig) functions does not change the % uncertainty of the result. If v = 2.36 m/s 3.1 % and t = 0.4567 1.1 %, then a = v/t= m/s % If the height of a ramp, h is 3.55 0.3 cm and length of the ramp, I is 25.60 0.2 cm, calculate the angle of incline, e: sin 0 = + % Q = arcsin (sin 0) = % Reading Uncertainty The source of uncertainty you will come across often in these labs is called reading uncertainty. It is determined by how precisely you can read a value off a scale. For this course, the reading uncertainty can be taken to be of the smallest scale division on the instrument that the measurement in question is being taken on. Ruler and Protractor Measurements When you take a measurement of length with a ruler (or an angle with a protractor), you have two reading uncertainties involved. One of them comes from reading the measurement off of the ruler (or protractor), and the other comes from lining up the starting position of the measurement with zero on your ruler (or protractor). Because of this, when measuring a length with a ruler that has small divisions (e.g., 0.1cm), it is appropriate to choose your uncertainty as follows: 2 ( the smallest division) = 2 (0.05 cm) = 0.1 cm If you're very careful, you could argue that the value can be read to the nearest 1/4 of the smallest division and therefore, the uncertainty for a length could be given as: 2 (1/4 the smallest division) = 2 (0.025 cm) = 0.05 cm (as seen in the example above) It's probably safer to go with the 0.1 cm, but the choice is yours. The important thing is that you can reasonably justify your estimate. 6) Sometimes the uncertainty is given in % form. If not, then you will be required to calculate a % uncertainty for each measurement. For A SA, A is the value SA is the uncertainty of A SA -x100% A is the percent uncertainty of A It is standard to state % uncertainties to 1-2 significant figures. If the book in Question 5) is measured to be 10.65 cm, what is the % uncertainty of the book? 7) How tall are you (measure your height with a tape measure)? cm Estimate an uncertainty for the measurement of your height? cm Justify why this uncertainty is higher than the uncertainty of the length of the book: Your height, h = + cm. cm %. % 3 L Physical Uncertainty Sometimes the quantity you are measuring has an intrinsic uncertainty in addition to the reading uncertainty of the device you are using to measure it. For example, if you try to measure the length of a cotton ball, the "fuzziness" of the cotton ball is where most of your uncertainty comes from - not the precision of the ruler. Your ruler might be subdivided into 0.1 cm divisions, but because the cotton ball has a poorly defined edge (i.e., it's "fuzzy"), your physical uncertainty might be another 0.1 cm or even more. Another example would be trying to measure how far a cart rolls up a hill before it reverses direction. The fact that the cart only pauses for an instant at the place where you need to take your measurement can make it difficult to see the exact location that the cart turns around at. This will increase your uncertainty for that measurement. Again, your ruler might have 0.1 cm divisions, but your physical uncertainty could be another 0.5 cm or even more (depending on the measurement/experiment). Instrument Uncertainty The instrument you are taking a measurement with may contain a built-in uncertainty that has nothing to do with your ability to read the device or the physical uncertainty. A device with a digital display has no (or little) reading uncertainty, but the device still has uncertainty usually found in the manufacturer's specifications. The instrument uncertainty can be much larger or much smaller than the smallest digit on the display. In these labs, instrument uncertainties are given to you in the Apparatus section of each lab. For example, the statistics given by the IoLab software will be given to you in the Apparatus section of the lab whenever you will be using the IOLab software to measure things. The statistics given by the IOLab software have an uncertainty of 3%. Choose an uncertainty for the measurement of the length of a book using your tape measure: cm. Provide a justification for your choice: Choose the best velocity-time graph for this description of motion 5) Fully label/describe every measurement you take. Also, include its units, estimate an uncertainty and justify your uncertainty estimate. Example of a measurement recorded correctly with uncertainty and the justification of the uncertainty: Written description Symbol Measurement _ Estimated uncertainty Length of wooden block, L = 12.20 0.15 cm Unit (2mm)=0.05 cm reading uncertainty due to reading both ends of ruler. 0.10 cm physical uncertainty due to roughness of block. Explanation of uncertainty estimate There are many types uncertainty, but the uncertainty that you estimate for any given measurement should be large enough to account for all of them. Here, we outline some common sources of uncertainty. You must combine the various uncertainties to get the total uncertainty for an individual measurement.