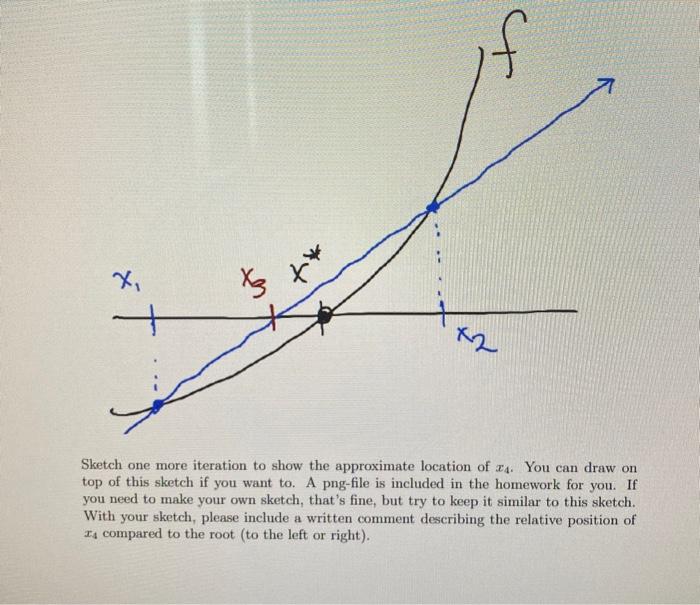
1. I would like to know when 2* = -1. Let's implement bisection by-hand to help us practice the algorithm. After completing this, you may work on the code for bisect.n in MGHW5. (a) (2 points) Rephrase this algebraic nonlinear equation as a root finding problem. (b) (15 points) Implement a few steps of the bisection method using pencil, paper, and a calculator. Start with the interval (-1,0). As a stopping criteria, your final interval should be less than 0.2 in length. Report your final approximation as the midpoint of this interval. Be sure to clearly indicate why you stopped iterating when you did. After completing this, you may work on the code for bisection.m in MGHW5. 2. (15 points) Newton by-hand. Implement Newton's method with pencil, paper, and a calculator to approximate a root of f(x) = re cos(0). Set your calculator in radian mode! Use I1 = 1. Stop iterating when the difference between successive approximations is less than 0.1. Be sure to clearly indicate why you stopped iterating when you did. After completing this, you may work on the code for myNewton.m in MGHW5. 3. (0 points) Complete MGHW5. Note that when implementing the code for myNewton.m, we stop when successive iterations are close. You can follow the procedure we took when we introduced while loops to compute a limit on January 29 (and the associated pre-class lecture and quiz!). You also practiced this procedure on MGHW3 on the Ricker problem. The code for secant.m is very similar to the code for my Newton.m. The difference is you have to keep track two previous iterations to make an update. There are several alternative and correct approaches to handling this in Matlab. 4. (8 points) Below is a partial picture of one iteration of secant method from the pre-class video: X Xg Sketch one more iteration to show the approximate location of 24. You can draw on top of this sketch if you want to. A png-file is included in the homework for you. If you need to make your own sketch, that's fine, but try to keep it similar to this sketch. With your sketch, please include a written comment describing the relative position of Il compared to the root (to the left or right)