1. Imagine that the production function for tuna cans is given by: q = 6K + 4L Where q = output of tuna cans per hour K = capital per hour L = labor input per hour. Assume capital is fixed at K = 6, how much L is required to produce 60 tuna cans per hour?

a. Now assume capital is fixed at K = 8, how much L is required to produce 100 tuna cans per hour?

b. Graph the q = 60 and q = 100 isoquants, in indicate the points found in parts a and b.

c. What is the MP of capital and labor?

d. What is the MRTS along the isoquants?

2. A perfectly competitive market has 1,000 firms. In the very short run, each of the firms has a fixed supply of 100 units. The market demand is given by: Q = 160,000 - 10,000P

a. What is the market supply curve in the very short run?

b. Calculate the equilibrium price in the very short run.

c. Calculate the demand schedule facing any one firm in the industry. Calculate what the equilibrium price would be if one of the sellers decided to sell nothing or if one seller decided to sell 200 units. What is concluded about the effect of any one firm on market price?

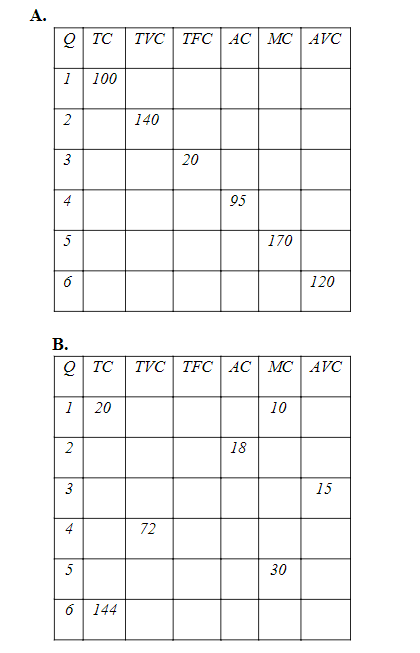
3. The following incomplete table shows a firm's various costs of producing up to 6 units of output. Fill in as much of the table as possible. If you cannot determine the number in a box, explain why it is not possible to do so. (Please show all workings)