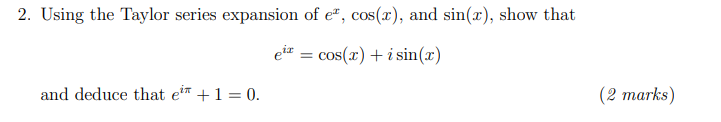
1. In the lectures, we skipped over showing that the function (1+x) was actually equal to the Taylor series n=0 (1) In principle, we needed to show that the remainder term vanished but this turns out to be very difficult. Instead, we can try something else: (a) The series in (1) is some function of x, as long as it converges. Let's call it g(x). Differentiate the function g(x), show that the resulting series g'(x) satisfies (1+x)g'(x) = kg(x), and give its radius of convergence. Hint: you can treat the left-hand side as multiplying polynomials term-by-term. You may make use of the identities: k - - n = k + = n n- n n- 1 = 1, = k. (4 marks) (b) Now, introduce a new function h(x) = (1+x)g(x). Show that h'(x) = 0. (2 marks) (c) Using the previous result, deduce that g(x) = (1+x), showing that indeed this function is equal to its Taylor series. Hint: What functions have a zero derivative for all values of x where they are defined? (2 marks) 2. Using the Taylor series expansion of e, cos(x), and sin(x), show that eix cos(x)+isin(x) = and deduce that ex+1 = 0. (2 marks)