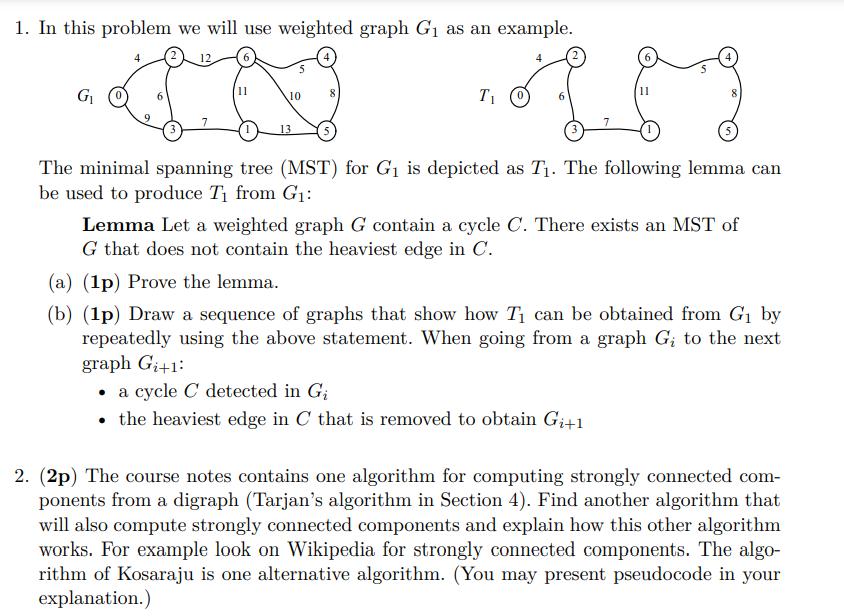
1. In this problem we will use weighted graph G as an example. G 12. 11 10 13 11 T O The minimal spanning tree (MST) for G is depicted as T. The following lemma can be used to produce T from G: Lemma Let a weighted graph G contain a cycle C. There exists an MST of G that does not contain the heaviest edge in C. (a) (1p) Prove the lemma. (b) (1p) Draw a sequence of graphs that show how T can be obtained from G by repeatedly using the above statement. When going from a graph G; to the next graph Gi+1: a cycle C detected in Gi the heaviest edge in C that is removed to obtain G+1 2. (2p) The course notes contains one algorithm for computing strongly connected com- ponents from a digraph (Tarjan's algorithm in Section 4). Find another algorithm that will also compute strongly connected components and explain how this other algorithm works. For example look on Wikipedia for strongly connected components. The algo- rithm of Kosaraju is one alternative algorithm. (You may present pseudocode in your explanation.)