1.

Let denote the usual parameter of the Poisson distribution.

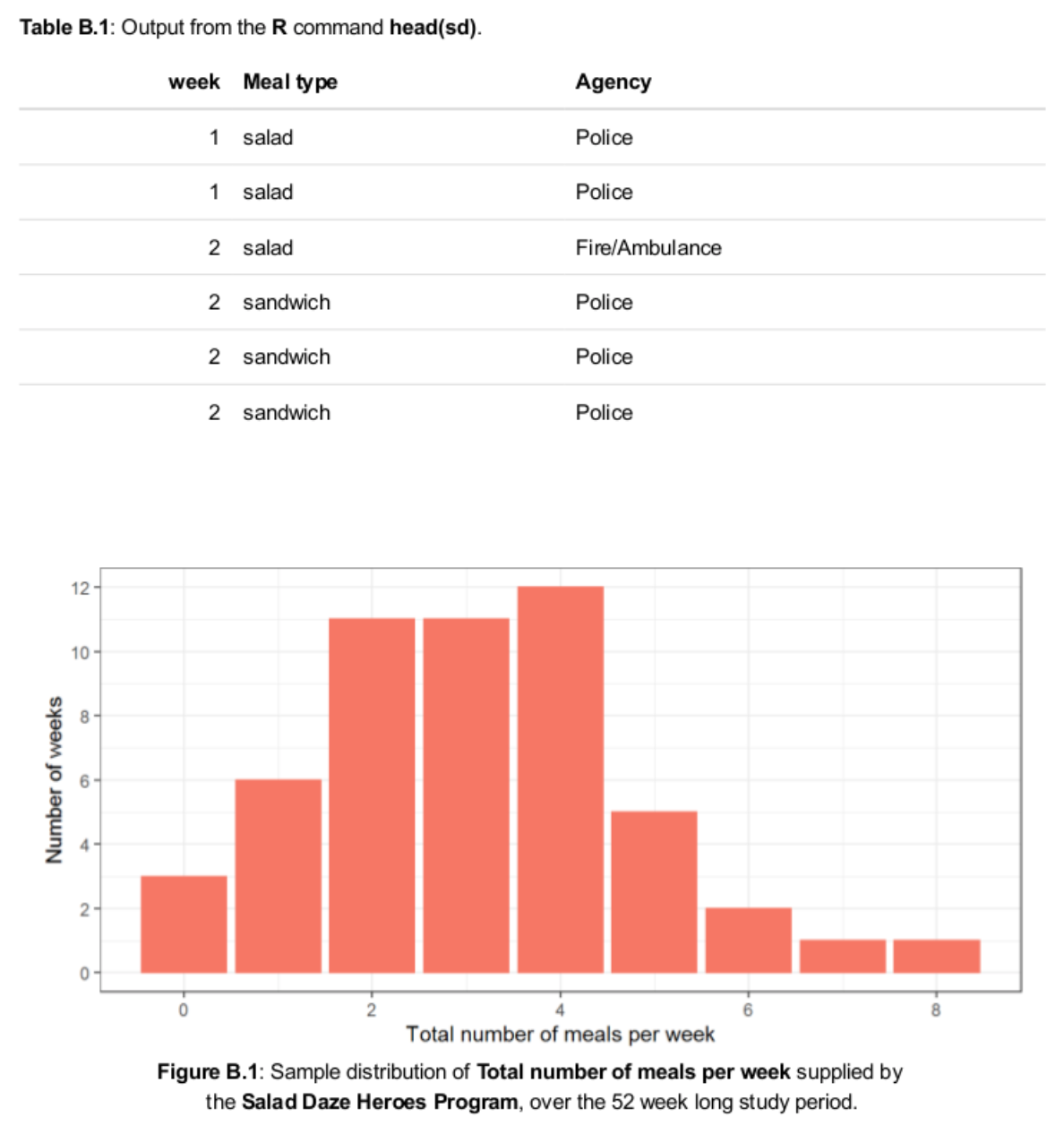
The approximate sampling distribution of ^MLE, as estimated using the available =52n=52data values representing theTotal number of meals per weeksupplied by theHeroes Program, is a Normal distribution, with mean equal to 2.982 and variance equal to (0.2352)/161.

T/F

2.

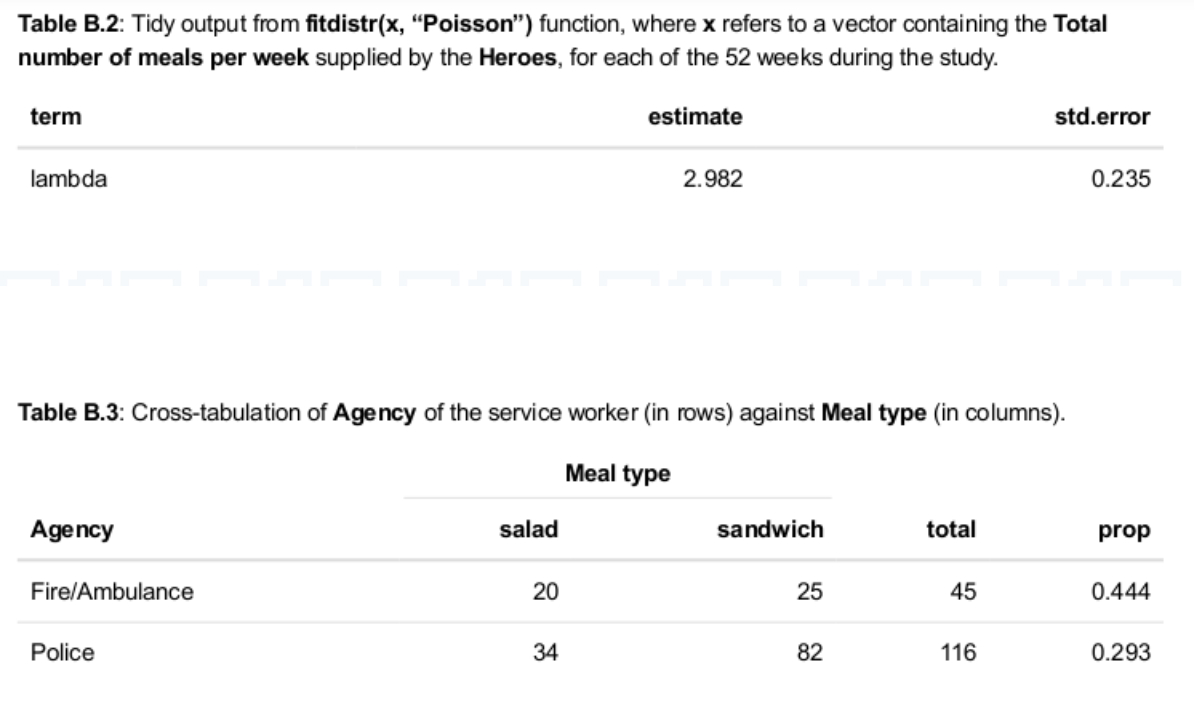
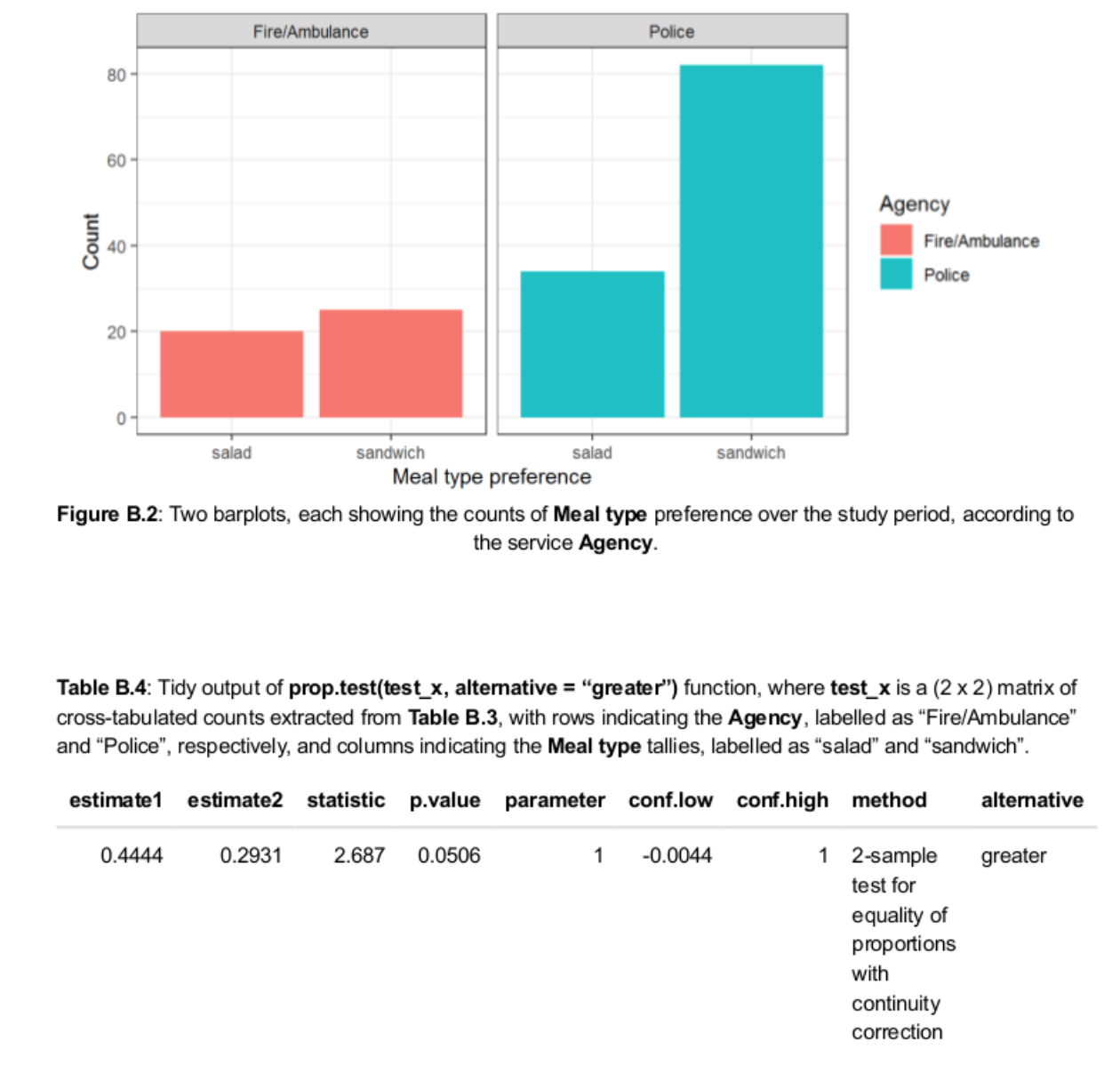
The output from theprop.test()function shown inTable B.4indicates that Fire/Ambulance service workers are more likely to choose a salad (instead of a sandwich) than are Police service workers.

T/F

3.

Which of the following statements isTRUE?

Select one:

a. The MLE-based forecast distribution for theTotal number of meals per weekprovided by theHeroesprogram, corresponding to the first week after the end of the sample period is a (=2.982)Poisson(=2.982) distribution.

b. When evaluated at the Maximum Likelihood Estimator, ^MLE, the log-Likelihood function has the same value as the Likelihood function.

c. The application of theprop.test()function, resulting in the output reported inTable B.4, is based on a regression model where the dependent variable is theTotal number of salad meals, and the independent variable is theTotal number of sandwich meals.

d. A Bootstrap-based confidence interval could be constructed for/pF/ApP.

6.

Again consider using a()

distribution to model the available=52

observations representing theTotal number of meals per weeksupplied to emergency service workers by theHeroes Program.Sally advises that before she started theHeroes Program, she expected to serve about 5 meals per week, on average. She also had anticipated that this average number of lunches per week could be different than five, but felt that there was a 90% chance that the average number of meals would be between one and eight.You therefore suggest to Sally that she adopt a Gamma distribution withshapeparameter=5

andrateparameter=1

, as this distribution is consistent with her stated prior belief. Sally is very happy to know this! And asks you to determine the posterior distribution for

now that the data has been collected.

Report the specific form of Sally's posterior distribution, and provide a justification for your answer.

[Note: You arenotrequired to formally derive the general form of the posterior distribution, rather you will need to identify the specific form of this distribution.]

Given the posterior distribution of

as detailed in Question 13, what is theBayes estimatorof

under the squared error loss function? Explain how to calculate its value in this context.

Table B.1: Output from the R command head(sd). week Meal type Agency 1 salad Police 1 salad Police 2 salad Fire/Ambulance 2 sandwich Police 2 sandwich Police 2 sandwich Police 12- 10 Number of weeks 6- N alll-. 2 Total number of meals per week Figure B.1: Sample distribution of Total number of meals per week supplied by the Salad Daze Heroes Program, over the 52 week long study period.Table B.2: Tidy output from fitdistrx, "Poisson") function, where x refers to a vector containing the Total number of meals per week supplied by the Heroes, for each of the 52 weeks during the study. term estimate std.error lambda 2.982 0.235 Table B.3: Cross-tabulation of Agency of the service worker (in rows) against Meal type (in columns). Meal type Agency salad sandwich total prop Fire/Ambulance 20 25 45 0.444 Police 34 82 116 0.293Fire/Ambulance Police 80 60 Agency Count 40 Fire/Ambulance Police 20 - salad sandwich salad sandwich Meal type preference Figure B.2: Two barplots, each showing the counts of Meal type preference over the study period, according to the service Agency. Table B.4: Tidy output of prop.test(test_x, alternative = "greater") function, where test_x is a (2 x 2) matrix of cross-tabulated counts extracted from Table B.3, with rows indicating the Agency, labelled as "Fire/Ambulance" and "Police", respectively, and columns indicating the Meal type tallies, labelled as "salad" and "sandwich". estimate1 estimate2 statistic p.value parameter conf.low conf.high method alternative 0.4444 0.2931 2.687 0.0506 1 -0.0044 1 2-sample greater test for equality of proportions with continuity correction