1. Let K_n be the complete graph on n vertices and K_m,n be the complete bipartite graph on m and n vertices. Find the number of vertices of each graph.

-	K3, 4
-	, 2
-	K5
-	K6

A.	9
B.	14
C.	5
D.	None of these
E.	6
F.	7
G.	12

2. Let K_n be the complete graph on n vertices and K_m,n be the complete bipartite graph on m and n vertices. Find the number of edges of each graph.

-	K5
-	K4
-	K2, 3
-	K3, 3

A.	9
B.	20
C.	6
D.	10
E.	None of these
F.	10
G.	5

3. A cycle is a closed path in which no vertex is repeated except the first and last. Using the graph G in Fig8-36(b), p.178, find the number of cycles through the vertex

 

-	A
- .	B
-	C
-	D

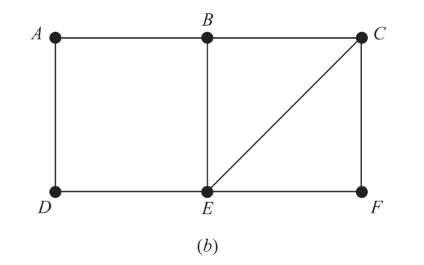
A.	4
B.	5
C.	2
D.	7
E.	None of these
F.	3
G.	6

4. A simple path from a vertex x to a vertex y is a path from x to y such that no vertex and hence no edge, is repeated. For the graph G in Fig 8-36(b), p.178, find the number of simple paths

 

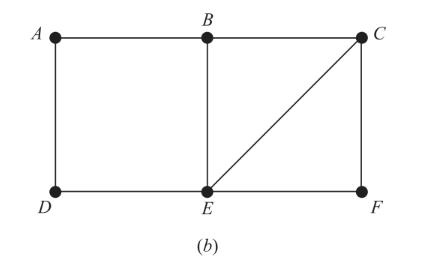
-	from A to F
-	from F to A
-	from B to C
-	from C to D

A.	5
B.	3
C.	4
D.	None of these
E.	6
F.	8
G.	7

5. A planar graph G = (V, E) has V = {1,2,3,4,5,6} and E = {{1,2},{1,3},{1,4},{1,5},{1,6},{2,3},{3,4},{4,5},{5,6},{6,2}}. Find

-	the number of regions (faces)
-	the number of edges
-	the diameter of G
-	sum of degrees of vertices

A.	18
B.	10
C.	6
D.	20
E.	2
F.	15
G.	None of these

A D B E (b) C F