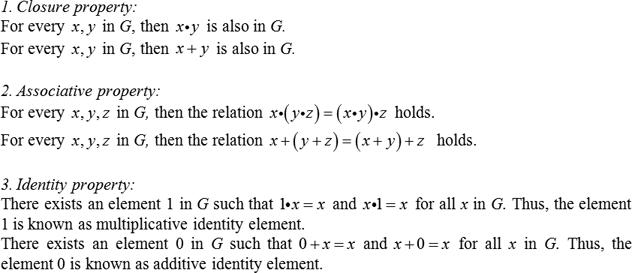
1. Closure property: For every x, y in G, then xy is also in G. For every x, y in G, then x+y is also in G. 2. Associative property: For every x, y, z in G, then the relation x(yz) = (xy)z holds. For every x, y,z in G, then the relation x+ (y+z)3 (x+y)+z holds. 3. Identity property: There exists an element 1 in G such that 1x = x and x-l=x for all x in G. Thus, the element 1 is known as multiplicative identity element. There exists an element 0 in G such that 0+x=x and x+0 =x for all x in G. Thus, the element 0 is known as additive identity element.