









1.
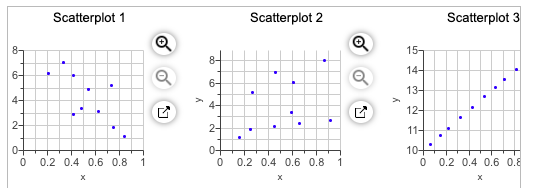
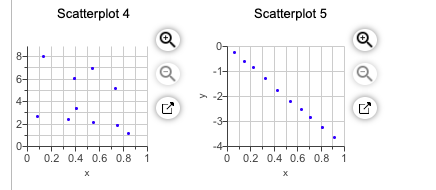
Match these values of r with the accompanying scatterplots: 0.372, 1, - 1, - 0.372, and -0.718. Click the icon to view the scatterplots. Match the values of r to the scatterplots. Scatterplot 1, r= Scatterplot 2, r= Scatterplot 3, r= Scatterplot 4, r= Scatterplot 5, r=Scatterplot 1 Scatterplot 2 Scatterplot 3 15 8 6 6 a 14- 13- 4- J A 12- 2 2 11- # 0 0 10- 0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8Scatterplot 4 Scatterplot 5 O 3 -2- -3- 0 -4 0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1 XFifty-four wild bears were anesthetized, and then their weights and chest sizes were measured and listed in a data set. Results Correlation Results are shown in the accompanying display. Is there sufficient evidence to support the claim that there is a linear correlation between Correlation coeff, r: 0.979642 the weights of bears and their chest sizes? When measuring an anesthetized bear, is it easier to measure chest size than weight? If so, does it appear that a measured chest size can be used to predict the weight? Use a significance level of a = 0.05. Critical r: + 0.2680855 P-value (two tailed): 0.000Identify the correlation coefficient, r. rE Round to three decimal places as needed.)Construct a scatterplot. Choose the correct graph below. O A. OB. O C. OD. 210- 2107 210- 200- 2107 200- 200- 190- 200- 190- Height (cm) 190- Height (cm) 180- 190- Height (cm) 180- Height (cm) 180- 170- 180- 170- 170- 160- 170- 160- 20 24 28 32 36 40 160- 20 24 28 32 36 40 160- 20 24 28 32 36 40 Shoe Print Length (cm) 20 24 28 32 36 40 Shoe Print Length (cm) Shoe Print Length (cm) Shoe Print Length (cm)The linear correlation coefficient r is| (Round to three decimal places as needed.) Determine the null and alternative hypotheses. Ho: P H1 : P (Type integers or decimals. Do not round.) The linear correlation coefficient r is (Round to three decimal places as needed.) Determine the null and alternative hypotheses. Ho: P H1 : P (Type integers or decimals. Do not round.) The test statistic is (Round to two decimal places as needed.) The P-value is. (Round to three decimal places as needed.) Because the P-value of the linear correlation coefficient is the significance level, there sufficient evidence to support the claim that there is a linear correlation between shoe print lengths and heights of males.Different hotels in a certain area are randon'ly selected, and their ratings and prices were obtained online. Using technology, with 1 representing the ratings and 3 representing price. we nd that the regression equation has a slope of 140 and a yintercept of - 392. Complete parts (a) and {b} below. a. What is the equation of the regression liI'Ie'iI Select the correct choice below and ll in the answer boxes to complete your choice. m awn]: 0\" V=D+i A 0- awn: on. v=D+l b. What does the symbol y represent? O A. The symbol y represents the average price of hotels in the area. B. The symbol y represents the amount that price increases with a 1-point increase in ratingCritical Values of the Pearson Correlation Coefficient r n o = 0.05 of = 0.01 NOTE: To test Ho: p = 0 0.950 0.990 against H: p #0, reject 5 0.878 0.959 Ho if the absolute value of 0.811 0.917 r is greater than the critical 0.754 0.875 value in the table. 0.707 0.834 0.666 0.798 10 0.632 0.765 11 0.602 0.735 12 0.576 0.708 13 0.553 0.684 14 0.532 0.661 15 0.514 0.641 16 0.497 0.62317 0.482 0.606 18 0.468 0.590 19 0.456 0.575 20 0.444 0.561 25 0.396 0.505 30 0.361 0.463 35 0.335 0.430 40 0.312 0.402 45 0.294 0.378 50 0.279 0.361 60 0.254 0.330 70 0.236 0.305 80 0.220 0.286 90 0.207 0.269 100 0.196 0.256n a = 0.05 o = 0.01Suppose IQ scores were obtained for 20 randomly selected sets of twins. The 20 pairs of measurements yield x = 95.89, y = 96.4, r =0.870, P-value =0.000, and y = - 2.74 + 1.03x, where x represents the IQ score of the twin born second. Find the best predicted value of y given that the twin born second has an IQ of 95? Use a significance level of 0.05. Click the icon to view the critical values of the Pearson correlation coefficient r. The best predicted value of y is . (Round to two decimal places as needed.)Use the given data to find the equation of the regression line. Examine the scatterplot and identify a characteristic of the data that is ignored by the regression line. x 10 9 11 8 11 14 6 4 12 7 5 y 7.12 6.55 12.73 7.1 7.93 9.19 6.08 5.53 8.09 6.13 5.48 Create a scatterplot of the data. Choose the correct graph below. O A. OB. O C. OD. Ay Ay 25- 25- 25- 25- 203 20 20 15 15 15- 10 105 10 109 5- 5- 0 5 10 15 20 25 0 5 10 15 20 25 0 5 10 15 20 25 0 5 10 15 20 25Find the equation of the regression line. (Round the constant two decimal places as needed. Round the coefficient to three decimal places as needed.) Identify a characteristic of the data that is ignored by the regression line. O A. There is no trend in the data. O B. There is an influential point that strongly affects the graph of the regression line. O C. There is no characteristic of the data that is ignored by the regression line. O D. The data has a pattern that is not a straight line.The data show the bug chirps per minute at different temperatures. Find the regression equation, letting the first variable be the independent (x) variable. Find the best predicted temperature for a time when a bug is chirping at the rate of 3000 chirps per minute. Use a significance level of 0.05. What is wrong with this predicted value? Chirps in 1 min 849 1214 830 1037 997 1094 Temperature (OF) 69.1 88.8 67.9 82.3 84.3 88.9 What is the regression equation? y = [+x (Round the x-coefficient to four decimal places as needed. Round the constant to two decimal places as needed.)Fifty matched pairs of magnitude/depth measurements randomly selected from 10,594 earthquakes recorded in one year from a location in southern California. Find the best predicted depth of an earthquake with a magnitude of 0.7. Use a significance level of 0.05. Click the icon to view the earthquake measurements. Click here to view the critical values of the Pearson correlation coefficient, r. The regression equation is y = +x. (Round to one decimal place as needed.)








































