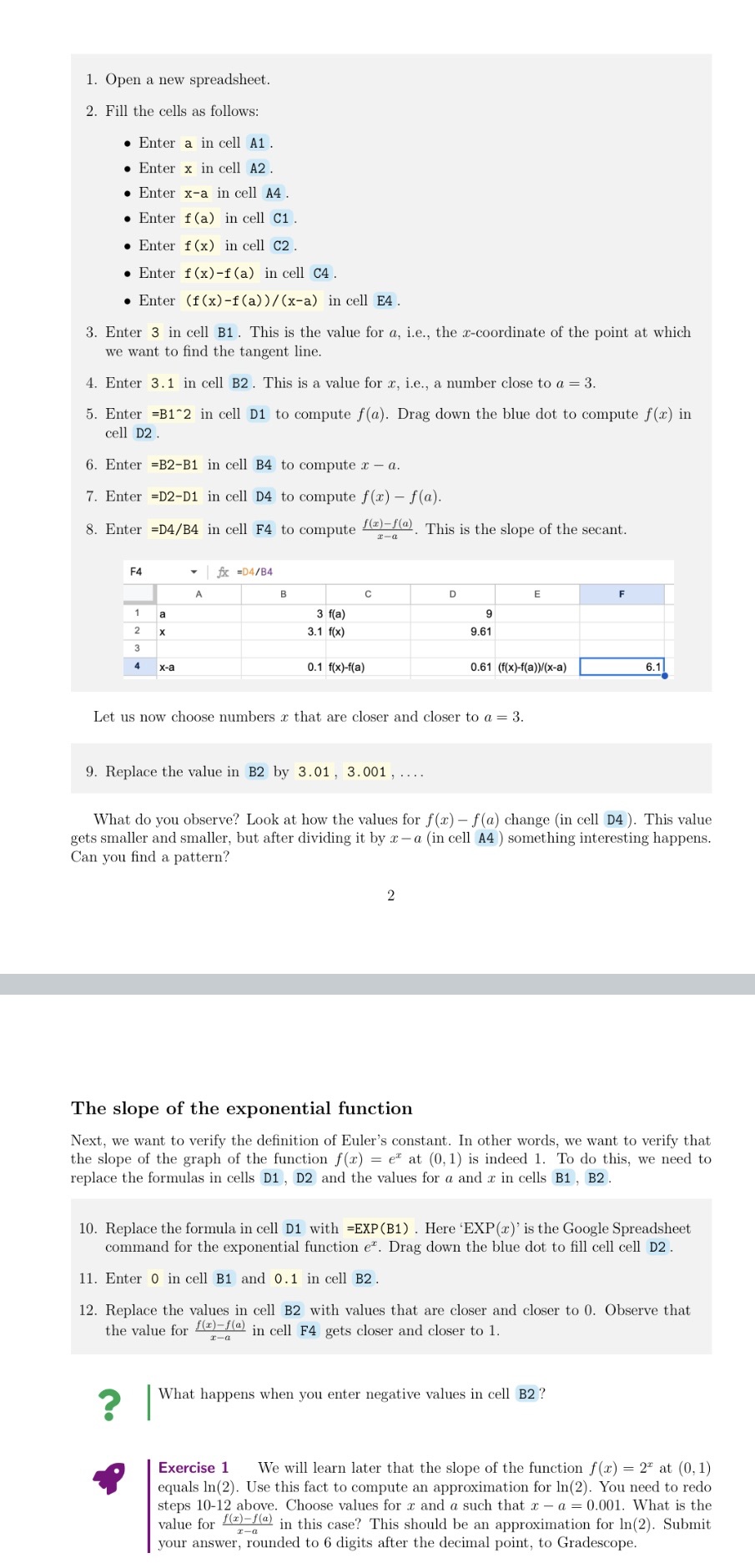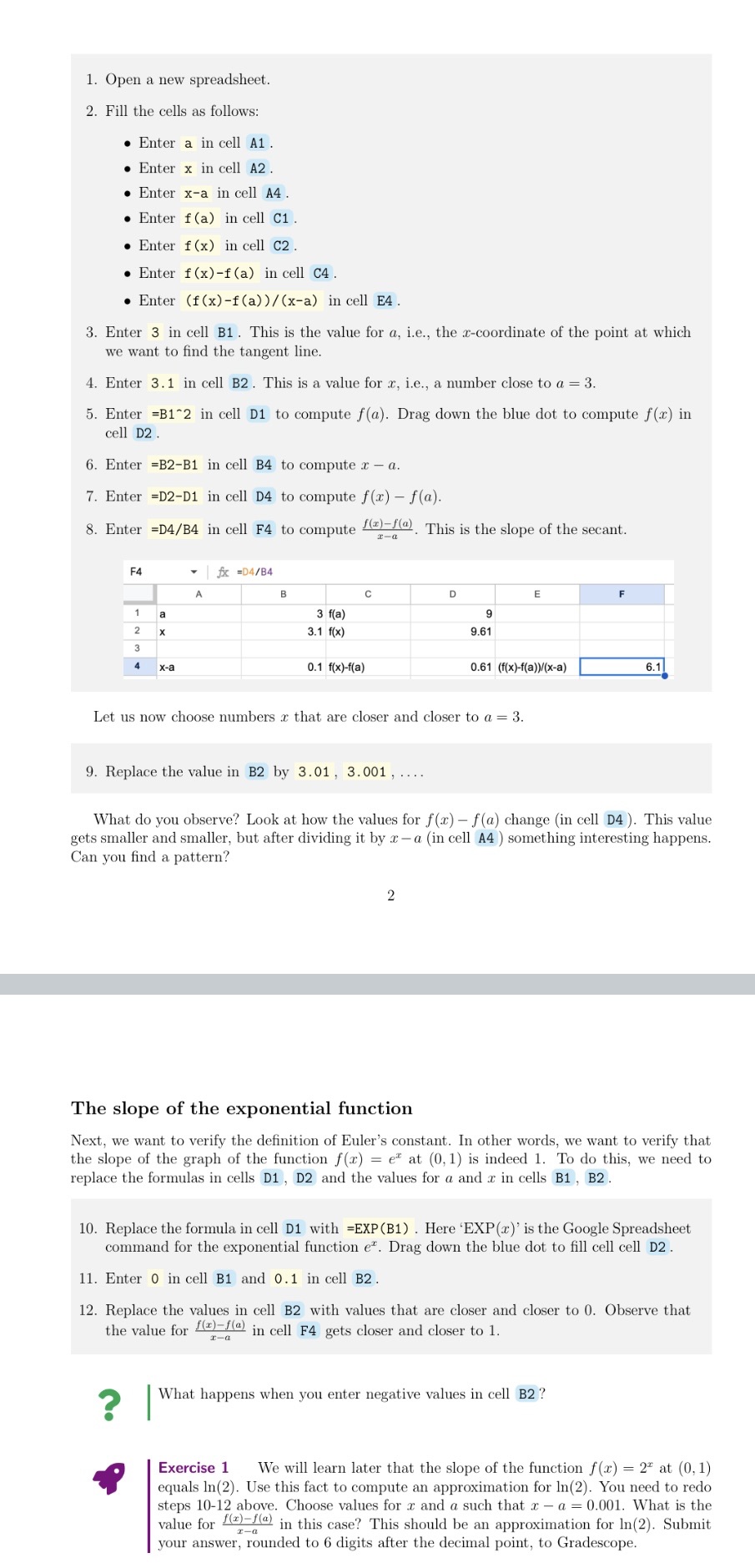
1. Open a new spreadsheet. 2. Fill the cells as follows: 0 Enter a in cell A1 . I Enter it in cell A2. 0 Enter x-a in cell A4. I Enter fta) in cell C1. 0 Enter f(x) in cell C2. o Enter f(x)-f(a) in cell C4. 0 Enter (I(x)-ft'a))/(x-a) in cell E4. 3. Enter 3 in cell 31 . This is the value for a, i.e., the m-coerdinate of the point at which we want to nd the tangent line. 4. Enter 3. 1 in cell B2 . This is a value for 1:. to, a number close to a : 3. 5. Enter =E|1"2 in cell D1 to compute e). Drag down the blue dot to compute f(.7;) in cell D2 . 6. Enter =B2-Bl in cell B4 to compute .ta, 7. Enter =D2-D1 in cell D4 to compute r) n). 8. Enter =D4/B4 in cell F4 to compute m. This is the slope of the secant. .ra F4 - fx = 'rea A E C D E F 3 file} 9 3.1 for) 9.51 xa 0.1 x)t(a) 0.51 (xmanxa) | 5.1. .5)! Let us now choose nnmhen: .11. that are closer and closer to a = 3. 9. Replace the value in B2 by 3.01 . 3.001 , \"mat do you observe? Look at how the values for f (.13) 7 e) change (in cell D4 ). This value gets smaller and smaller. but after dividing it by .1: a (in cell A4 ) something interesting happens. Can you nd a. pattern? The slope of the exponential function Next. we want to verify the denition of Euler's constant. In other words. we want to verify that the slope of the graph of the function f(.1) = e:r at (0.1} is indeed I. To do this, we need to replace the formulas in cells 01 ' D2 and the values for (t and J: in cells El . 32. 10. Replace the formula in cell DJ. with =EXP(31) . Here 'EXP(:)' isthe Goegle Spreadsheet command for the exponential function er. Drag down the blue dot to ll cell cell D2 . 11. Enter 0 in cell Bi and 0.1 in cell 132. 12. Replace the values in cell B2 with values that are closer and closer to 0. Observe that the value for $5? in cell F4 gets closer and clatter to 1. 9 I What happens when you enter negative values in cell B2 '.' . Exercise 1 \"'e will learn later that. the elope of the function HI) = 2' at (0.1) * equals 1M2). Use this feet to compute. an approximation for ln[2). You need to redo steps 1012 above. Choose values for .r and a such that .r. n : 0.001. What is the value for % in this case? This should he an approximation for 111(2). Submit. vnnr answer. rounded to (i digits after the decimal point. to GIRdE'HI'Upt