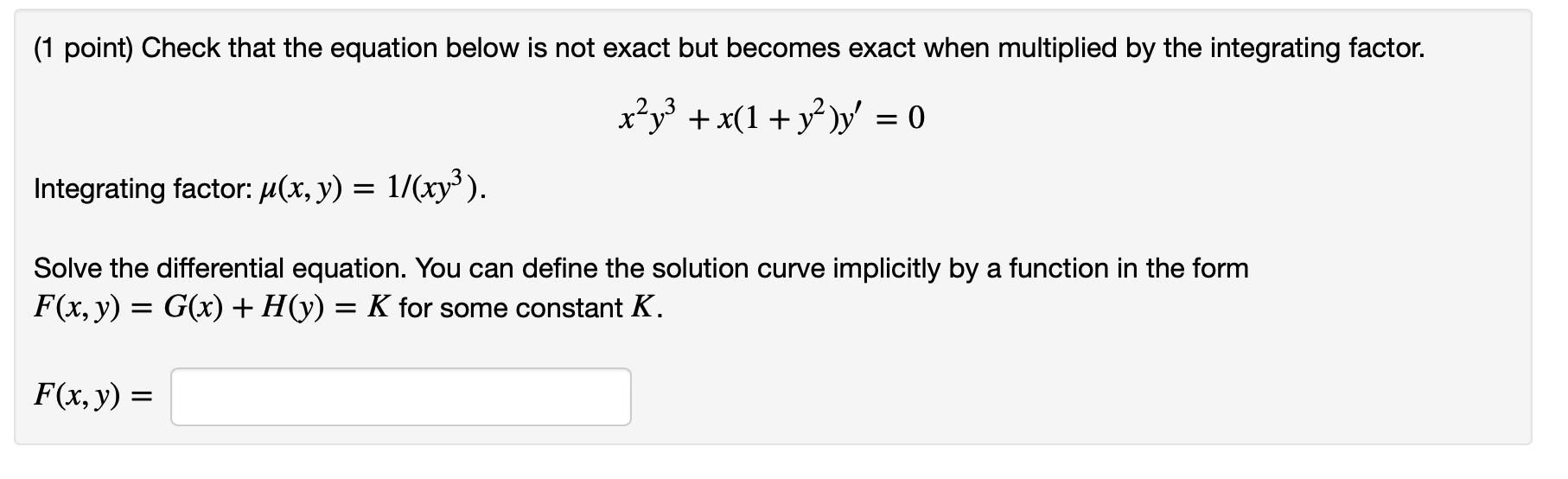
(1 point) Check that the equation below is not exact but becomes exact when multiplied by the integrating factor. xy +x(1 + y)y' = 0 Integrating factor: (x, y) = 1/(xy). Solve the differential equation. You can define the solution curve implicitly by a function in the form F(x, y) = G(x) + H(y) = K for some constant K. F(x, y) =