Answered step by step
Verified Expert Solution
Question
1 Approved Answer
(1 point) Suppose the sequence a(n) satisfies the following linear recurrence: a(n) = 6a(n 1) +5; a(0) = 6. (a) Find a closed (explicit)
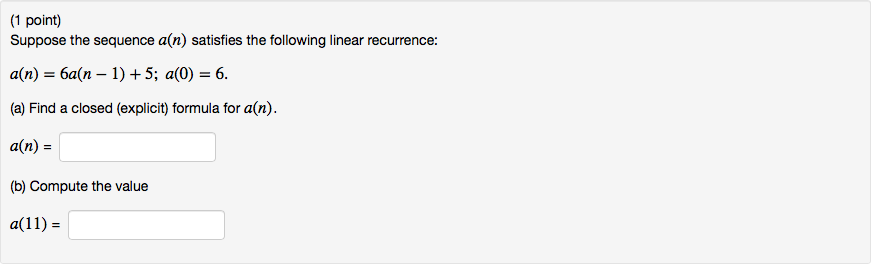
(1 point) Suppose the sequence a(n) satisfies the following linear recurrence: a(n) = 6a(n 1) +5; a(0) = 6. (a) Find a closed (explicit) formula for a(n). a(n) = (b) Compute the value a(11) =
Step by Step Solution
★★★★★
3.40 Rating (163 Votes )
There are 3 Steps involved in it
Step: 1
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2
Step: 3
Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started
Applied Linear Algebra
Authors: Peter J. Olver, Cheri Shakiban
1st edition
131473824, 978-0131473829
