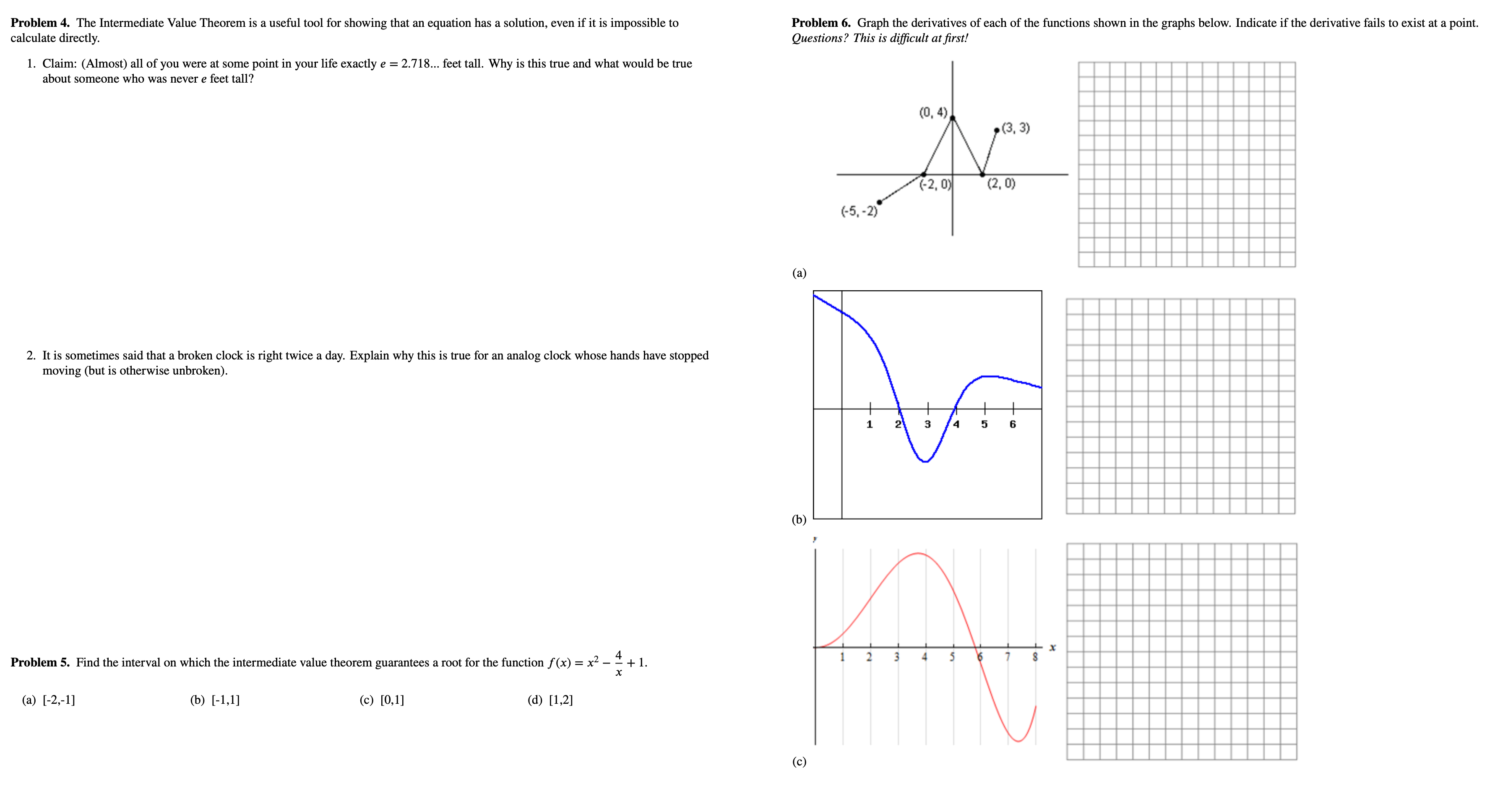
1 Problem 1. Determine where the function f (x) = 1 + sin x - is continuous on [0, 2x] Problem 2. Sketch 3 examples of graphs that have different types of discontinuities. Explain how each example violates the definition of continuity, being sure to identify the specific violation. Problem 3. 1. Find a value of c so that f (x) is continuous everywhere, where f (x ) = 1 x2 - 10, xSc 8x - 26 x > c 2. Fill in the blanks with digits 1-9, so that f(x) is continuous everywhere. You can use the same digit multiple times. How many solutions can you find? f ( x ) = { x2 - 17, x 5 0 [x - 29 x> 0Problem 4. The Intermediate Value Theorem is a useful tool for showing that an equation has a solution, even if it is impossible to Problem 6. Graph the derivatives of each of the functions shown in the graphs below. Indicate if the derivative fails to exist at a point. calculate directly. Questions? This is difficult at first! 1. Claim: (Almost) all of you were at some point in your life exactly e = 2.718... feet tall. Why is this true and what would be true about someone who was never e feet tall? (0, 4) (3, 3) (-2, 0) (2, 0) (-5, -2) (a) 2. It is sometimes said that a broken clock is right twice a day. Explain why this is true for an analog clock whose hands have stopped moving (but is otherwise unbroken). (b) Problem 5. Find the interval on which the intermediate value theorem guarantees a root for the function f (x) = x2 - 2 + 1. (a) [-2,-1] (b) [-1,1] (c) [0,1] (d) [1,2] (c)Problem 7. Use the definition of the derivative to find f'(4) for the function f (x) = 3x + 4 Problem 8. Use the definition of the derivative to find an equation for the tangent line to the curve y = vx at the point (1, 1) Problem 9. Use the definition of the derivative to find an equation for the tangent line to the hyperbola y = ~ at the point (3,1)