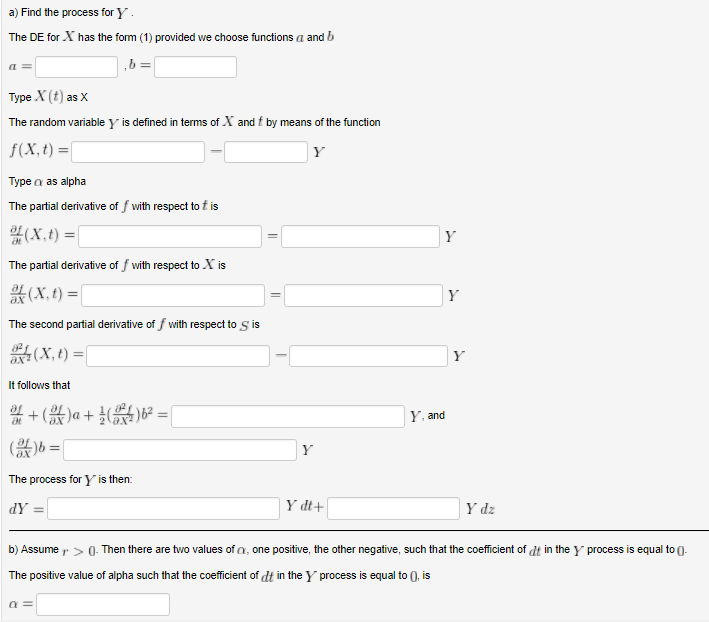
(1 pt) Changes in a variable such as stock price involve a deterministic component which is a function of time and a stochastic component which depends upon a random variable. Let S be the stock price at time t and let dS be the infinitesimal change in S over the infinitesimal interval of time dt. The change in the random variable z over this interval of time is dz. The change in stock price is given by (1) dS = adt +bdz where a and b may be functions of s and f. The expected value of dz is zero so the expected value of dS is equal to the deterministic component, a dt The random variable dz represents an accumulation of random influences over the interval dt The Central Limit Theorem then implies that dz has a normal distribution and hence is completely characterized by its mean and standard deviation. The mean or expected value of dz is zero. The variance of a random variable which is the accumulation of independent effects over an interval of time is proportional to the length of the interval, in this case dt The standard deviation of dz is thus proportional to dt All of this means that the random variable dz is equivalent to a random variable w(dt) i, where uw is a standard normal variable with mean zero and standard deviation equal to unity Now consider another variable C,such as the price of a call option, which is a function of S and t, say C- f(S,t). Because is a function of the stochastic variable S. will have a stochastic component as well as a deterministic component. will have a representation of the form: (2)dC = pdt+qdz The crucial problem is how the functions p and q are related to the functions a and b in the equation (1). Ito's Lemma gives the answer. The deterministic and stochastic components of dC are given by: ef (4),-() Ito's Lemma is crucial in deriving differential equations for the value of derivative securities such as stock options Suppose that X(t follows the process dX (t) = 2x (t)dt + x(t)dz where z is Brownian motion, and suppose that Y = e-rtXo, where r and are constants (1 pt) Changes in a variable such as stock price involve a deterministic component which is a function of time and a stochastic component which depends upon a random variable. Let S be the stock price at time t and let dS be the infinitesimal change in S over the infinitesimal interval of time dt. The change in the random variable z over this interval of time is dz. The change in stock price is given by (1) dS = adt +bdz where a and b may be functions of s and f. The expected value of dz is zero so the expected value of dS is equal to the deterministic component, a dt The random variable dz represents an accumulation of random influences over the interval dt The Central Limit Theorem then implies that dz has a normal distribution and hence is completely characterized by its mean and standard deviation. The mean or expected value of dz is zero. The variance of a random variable which is the accumulation of independent effects over an interval of time is proportional to the length of the interval, in this case dt The standard deviation of dz is thus proportional to dt All of this means that the random variable dz is equivalent to a random variable w(dt) i, where uw is a standard normal variable with mean zero and standard deviation equal to unity Now consider another variable C,such as the price of a call option, which is a function of S and t, say C- f(S,t). Because is a function of the stochastic variable S. will have a stochastic component as well as a deterministic component. will have a representation of the form: (2)dC = pdt+qdz The crucial problem is how the functions p and q are related to the functions a and b in the equation (1). Ito's Lemma gives the answer. The deterministic and stochastic components of dC are given by: ef (4),-() Ito's Lemma is crucial in deriving differential equations for the value of derivative securities such as stock options Suppose that X(t follows the process dX (t) = 2x (t)dt + x(t)dz where z is Brownian motion, and suppose that Y = e-rtXo, where r and are constants