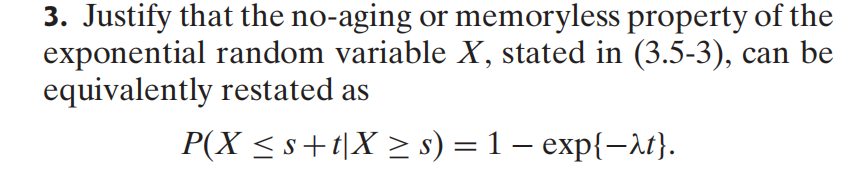
1. The lifespan of a car battery averages six years. Suppose the battery lifespan follows an exponential distribution. (a) Find the probability that a randomly selected car battery will last more than four years. (b) Find the variance and the 95th percentile of the bat- tery lifespan. (c) Suppose a three-year-old battery is still going strong. (i) Find the probability the battery will last an addi- tional five years. (ii) How much longer is this battery expected to last? 3. Justify that the no-aging or memoryless property of the exponential random variable X, stated in (3.5-3), can be equivalently restated as - P(X s+t|X s) = 1 exp{-t}.