1) Think of the network G=(N,A) as a highway map, and assume a cost of traversing each arc. Suppose that we incur an additional cost (or penalty) of 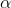units every time we make a left turn.

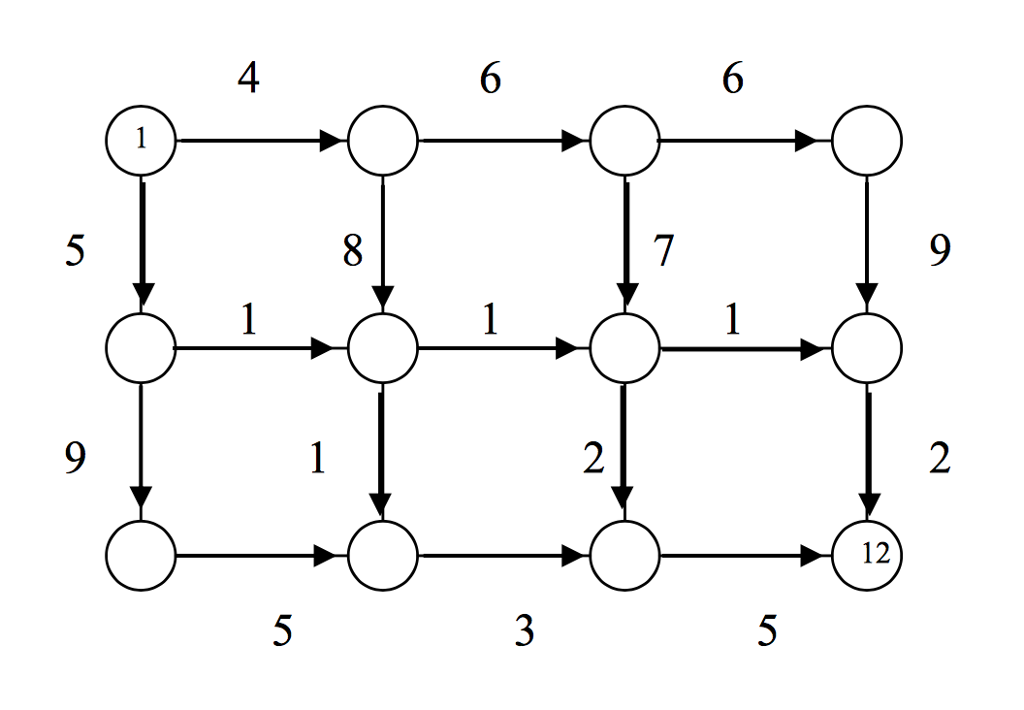
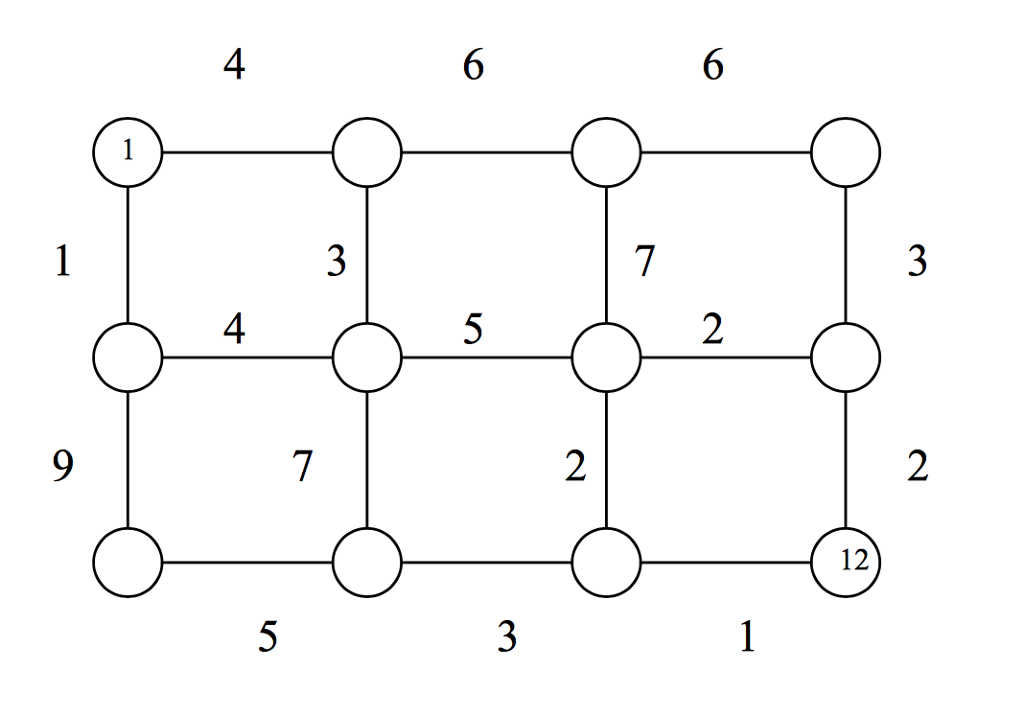
Formulate this problem as a shortest path problem. Hint: Create a new network G* with nodes (i-j) corresponding to each arc (i,j) 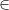A. Define appropriate arcs and arc lengths to the new network G*. As an instance consider the given network, and you want to find the shortest path from node 1 to node 12. What is G*? What is the shortest path and its distance on G*? (including a left turn penalty of 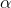? =10)?

2) Let c_ij ? 0 denote the capacity of an arc in a given network. Define the capacity of a directed path P as the minimum arc capacity in P. The maximum capacity path problem is to determine a maximum capacity path from a specified source node s to every other node in the network. Modify Dijkstras algorithm so that it solves the maximum capacity path problem. Justify your algorithm.

3) Consider the network given in problem 1, but this time the arc attributes are the maximum elevation encountered in traversing the arc. A traveler plans to drive from node 1 to node 12 on this highway. This traveler dislikes high altitudes and so would like to find a path, connecting node 1 to node 12, which minimizes the maximum altitude. Find the best path for this traveler. Describe the algorithm that you use in detail.