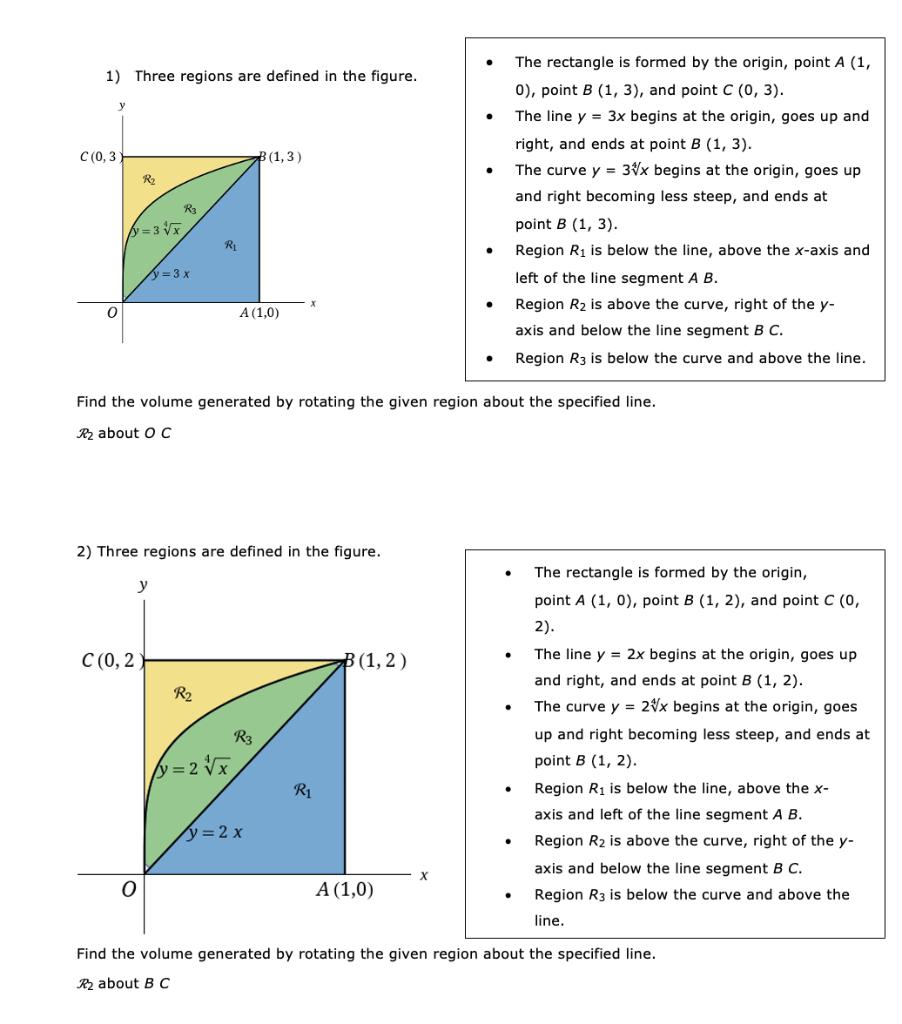
1) Three regions are defined in the figure. C (0,3 y 0 R y=3x R3 y y=3x C (0, 2) R 2) Three regions are defined in the figure. R A (1,0) y = 2x (1,3) Find the volume generated by rotating the given region about the specified line. R about O C R3 y=2x R B(1,2) A (1,0) . The rectangle is formed by the origin, point A (1, 0), point B (1, 3), and point C (0, 3). The line y = 3x begins at the origin, goes up and right, and ends at point B (1, 3). The curve y = 3x begins at the origin, goes up and right becoming less steep, and ends at point B (1, 3). Region R is below the line, above the x-axis and left of the line segment A B. Region R is above the curve, right of the y- axis and below the line segment B C. Region R3 is below the curve and above the line. The rectangle is formed by the origin, point A (1, 0), point B (1, 2), and point C (0, 2). The line y = 2x begins at the origin, goes up and right, and ends at point B (1, 2). The curve y = 2x begins at the origin, goes up and right becoming less steep, and ends at point B (1, 2). Region R is below the line, above the x- axis and left of the line segment A B. Region R is above the curve, right of the y- axis and below the line segment B C. Region R3 is below the curve and above the line. Find the volume generated by rotating the given region about the specified line. R2 about B C