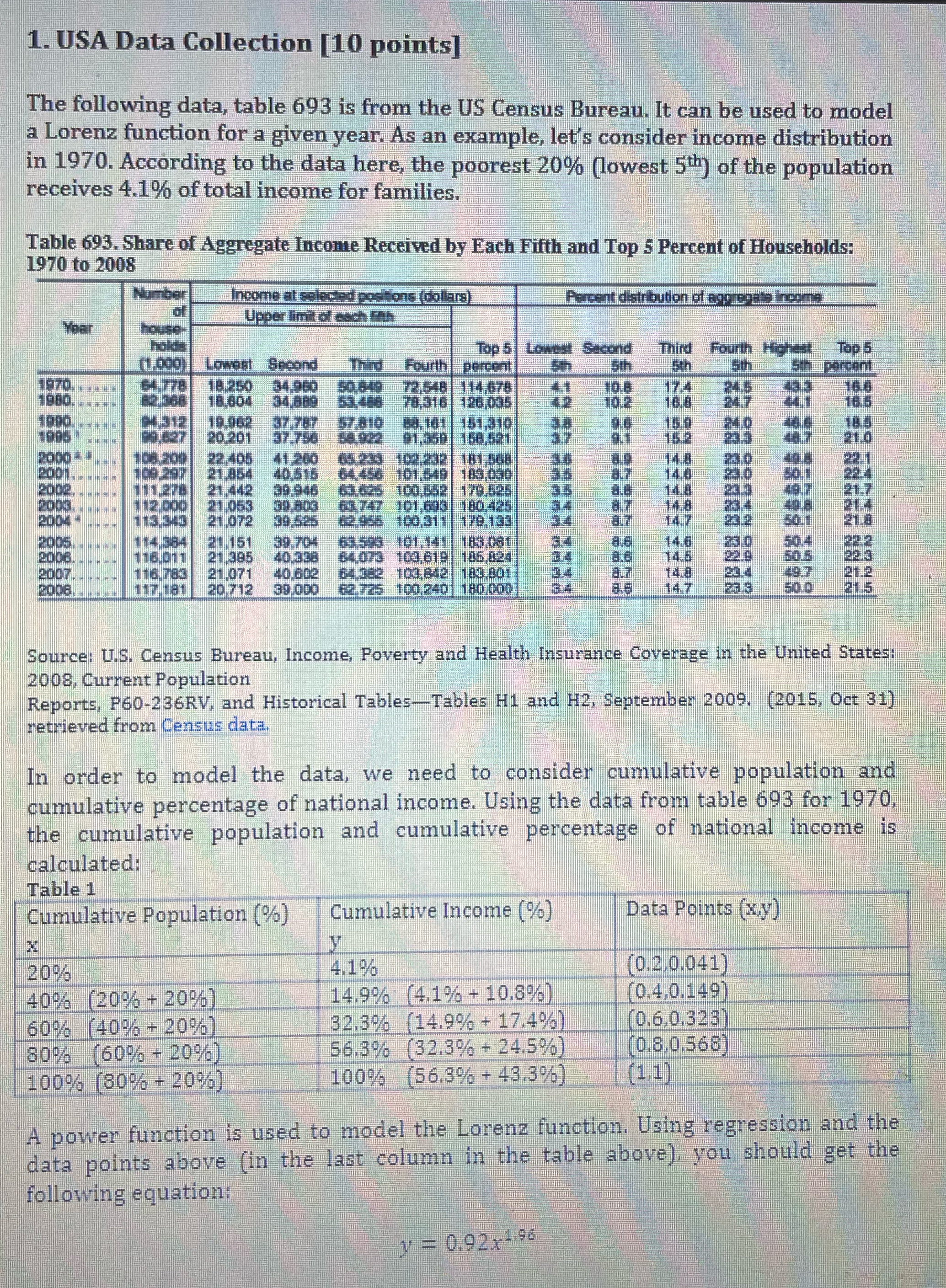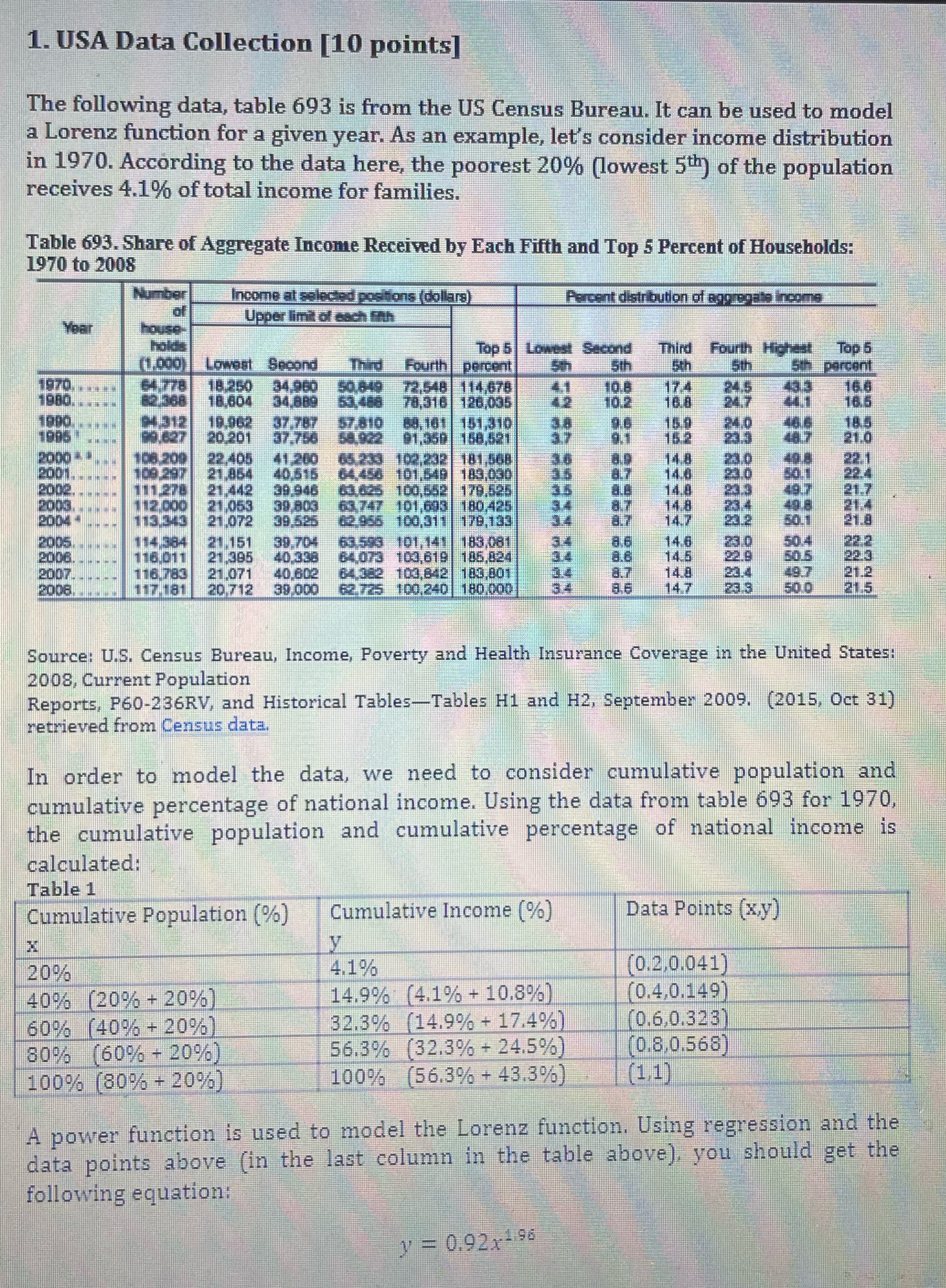
1. USA Data Collection [10 points] The following data, table 693 is from the US Census Bureau. It can be used to model a Lorenz function for a given year. As an example, let's consider income distribution in 1970. According to the data here, the poorest 20% (lowest 5th) of the population receives 4.1% of total income for families. Table 693. Share of Aggregate Income Received by Each Fifth and Top 5 Percent of Households: 1970 to 2008 Income at selected positions (dollars) Percent distribution of aggregate Income Upper limit of each fath Top 5 Second Third Fourth High Top 5 Lowest Spoond Thire Fourth |_percent 5th 5th percent 72.548 114,678 10 2 16.6 1980. 126,035 1610 151.310 20 20 158,521 21.0 2000 108 200 22.405 41,200 102.232 181,508 22. 2001. 21,864 40.51 101,840 183,090 3.0 22.4 2002. 21.442 39.946 100,682 179.525 14.4 23.3 21.7 2006 12 090 21,053 1,693 | 180.425 877 14 8 234 21.4 2004 21.072 179,135 34 1407 23.2 21.8 2005 21.151 39.704 101,141 183,081 3.4 8.6 146 230 504 22.2 2006, 116,01 1 21,305 40.33 103,619 185,824 34 8.6 145 22.9 50.5 22.3 2007 116 783 21.071 40.602 103,842 183,801 3.4 8.7 14.8 23.4 49.7 21. 2006. 1 17181 20 712 39.000 100.240 180,090 147 3.3 50.0 Source: U.S. Census Bureau, Income, Poverty and Health Insurance Coverage in the United States: 2008, Current Population Reports, P60-236RV, and Historical Tables-Tables H1 and H2, September 2009. (2015, Oct 31) retrieved from Census data. In order to model the data, we need to consider cumulative population and cumulative percentage of national income. Using the data from table 693 for 1970, the cumulative population and cumulative percentage of national income is calculated: Table 1 Cumulative Population (%) Cumulative Income (%) Data Points (x,y) X 20% 4.1% (0.2,0.041) 40% (20% + 20%) 14.9% (4.1% + 10.8%) (0.4,0.149) 60% (40% + 20%) 32.3% (14.9% + 17.4%) (0.6.0.323) 80% (60% - 20%) 56.3% (32.3% + 24.5%) (0.8.0.568) 100% (80% - 20%) 100% (56.3% + 43.3%) (1,1 ) A power function is used to model the Lorenz function. Using regression and the data points above (in the last column in the table above), you should get the following equation: = 0.92x- 96