
1- Use the implementation of BST.zip.Write a new function AVLTreeInsert in the Binary Search Tree class,which performs an insertion as in an AVL tree, hence keeping the tree balanced.Write auxiliary functions when necessary.
2-This part tests the code in the previous question.In the main function,Insert 10000 random integers using the usual insert of the Binary Search Tree class on one tree,and also using the AVLTreeInsert function on another tree.Compare the heights of the trees(You should anyway write a function computing the height of a tree).
All given C++ codes are below:(BST.zip have BST.h,BST.cpp,KeyedItem.h,main.cpp,TreeException.h,TreeNodeBST.h)
BST.zip (includes the following files below in c++):
BST.h:
// Header file BST.h for the ADT binary search tree. // Assumption: A tree contains at most one item with a given // search key at any time. // ********************************************************* #include "TreeException.h" #include "TreeNodeBST.h" typedef void (*FunctionType)(TreeItemType& anItem);
class BinarySearchTree { public: // constructors and destructor: BinarySearchTree(); BinarySearchTree(const BinarySearchTree& tree); virtual ~BinarySearchTree();
int height() const; int heightRecursive(TreeNode *root) const;
// binary search tree operations: // Precondition for all methods: No two items in a binary // search tree have the same search key.
virtual bool isEmpty() const; // Determines whether a binary search tree is empty. // Postcondition: Returns true if the tree is empty; // otherwise returns false.
virtual void searchTreeInsert(const TreeItemType& newItem); // Inserts an item into a binary search tree. // Precondition: The item to be inserted into the tree // is newItem. // Postcondition: newItem is in its proper order in the // tree.
virtual void searchTreeDelete(KeyType searchKey) throw(TreeException); // Deletes an item with a given search key from a binary // search tree. // Precondition: searchKey is the search key of the item // to be deleted. // Postcondition: If the item whose search key equals // searchKey existed in the tree, the item is deleted. // Otherwise, the tree is unchanged and TreeException // is thrown.
virtual void searchTreeRetrieve(KeyType searchKey, TreeItemType& treeItem) const throw(TreeException); // Retrieves an item with a given search key from a // binary search tree. // Precondition: searchKey is the search key of the item // to be retrieved. // Postcondition: If the retrieval was successful, // treeItem contains the retrieved item. // If no such item exists, throws TreeException.
virtual void searchTreeRetrieve(KeyType searchKey, TreeNode*& treeItem) const throw(TreeException);
virtual void preorderTraverse(FunctionType visit); // Traverses a binary search tree in preorder, // calling function visit() once for each item. // Precondition: The function represented by visit() // exists outside of the class implementation. // Postcondition: visit's action occurred once for each // item in the tree. // Note: visit() can alter the tree.
virtual void inorderTraverse(FunctionType visit); // Traverses a binary search tree in sorted order, // calling function visit() once for each item.
virtual void postorderTraverse(FunctionType visit); // Traverses a binary search tree in postorder, // calling function visit() once for each item.
// overloaded operator: virtual BinarySearchTree& operator=( const BinarySearchTree& rhs);
protected: void insertItem(TreeNode *& treePtr, const TreeItemType& newItem) throw(TreeException); // Recursively inserts an item into a binary search tree. // Precondition: treePtr points to a binary search tree, // newItem is the item to be inserted. // Postcondition: Same as searchTreeInsert.
void deleteItem(TreeNode *& treePtr, KeyType searchKey) throw(TreeException); // Recursively deletes an item from a binary search tree. // Precondition: treePtr points to a binary search tree, // searchKey is the search key of the item to be deleted. // Postcondition: Same as searchTreeDelete.
void deleteNodeItem(TreeNode *& nodePtr); // Deletes the item in the root of a given tree. // Precondition: nodePtr points to the root of a // binary search tree; nodePtr != NULL. // Postcondition: The item in the root of the given // tree is deleted.
void processLeftmost(TreeNode *& nodePtr, TreeItemType& treeItem); // Retrieves and deletes the leftmost descendant of a // given node. // Precondition: nodePtr points to a node in a binary // search tree; nodePtr != NULL. // Postcondition: treeItem contains the item in the // leftmost descendant of the node to which nodePtr // points. The leftmost descendant of nodePtr is // deleted.
void retrieveItem(TreeNode *treePtr, KeyType searchKey, TreeItemType& treeItem) const throw(TreeException); // Recursively retrieves an item from a binary search // tree. // Precondition: treePtr points to a binary search tree, // searchKey is the search key of the item to be // retrieved. // Postcondition: Same as searchTreeRetrieve. void retrieveItem(TreeNode *treePtr, KeyType searchKey, TreeNode*& treeNode) const throw(TreeException);
// The following 9 methods are the same as for the ADT // binary tree, and so their specifications are abbreviated. void copyTree(TreeNode *treePtr, TreeNode *& newTreePtr) const; void destroyTree(TreeNode *& treePtr);
void preorder(TreeNode *treePtr, FunctionType visit); void inorder(TreeNode *treePtr, FunctionType visit); void postorder(TreeNode *treePtr, FunctionType visit);
TreeNode *rootPtr() const; void setRootPtr(TreeNode *newRoot);
void getChildPtrs(TreeNode *nodePtr, TreeNode *& leftChildPtr, TreeNode *& rightChildPtr) const; void setChildPtrs(TreeNode *nodePtr, TreeNode *leftChildPtr, TreeNode *rightChildPtr);
private: TreeNode *root; // pointer to root of tree }; // end class // End of header file.
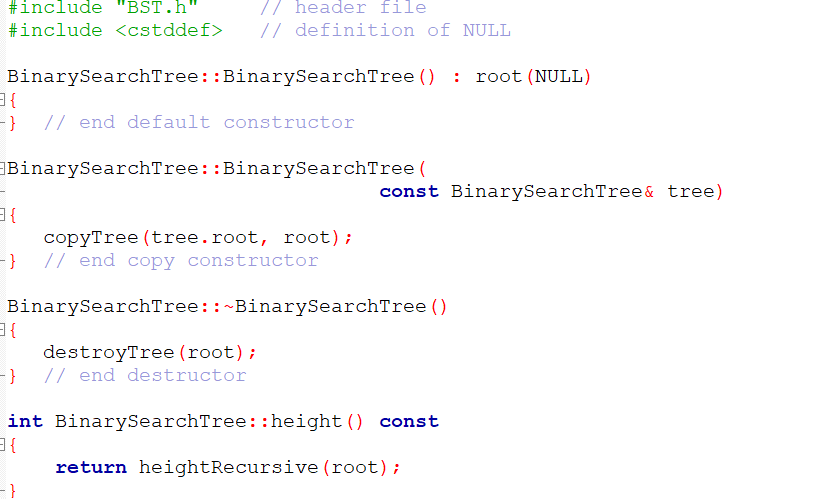
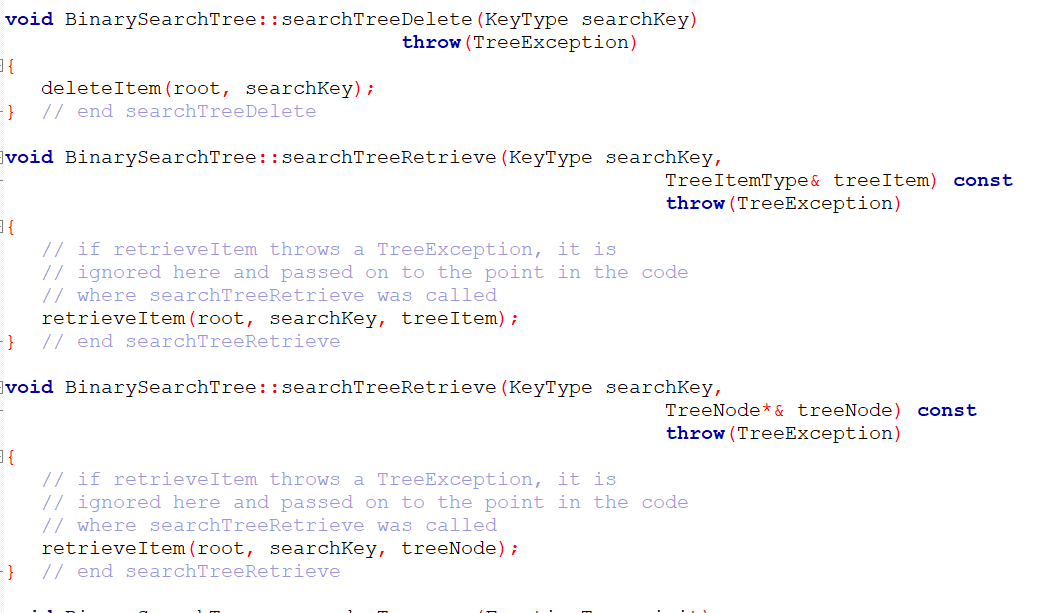
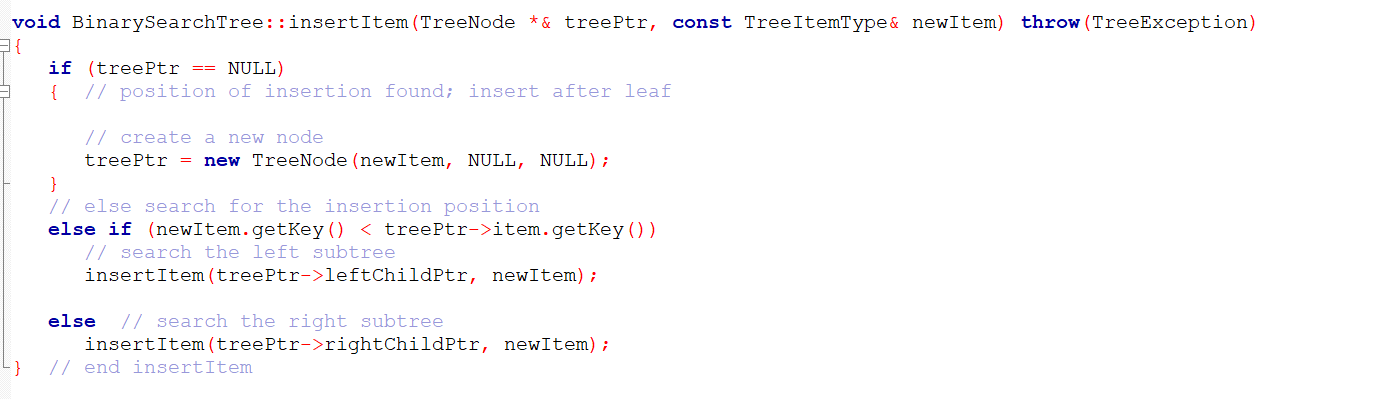
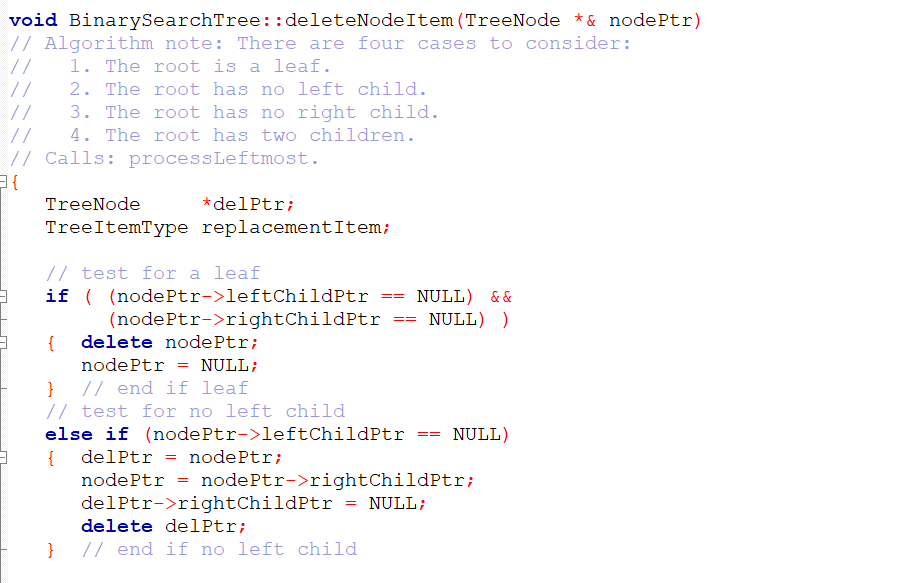
BST.cpp:





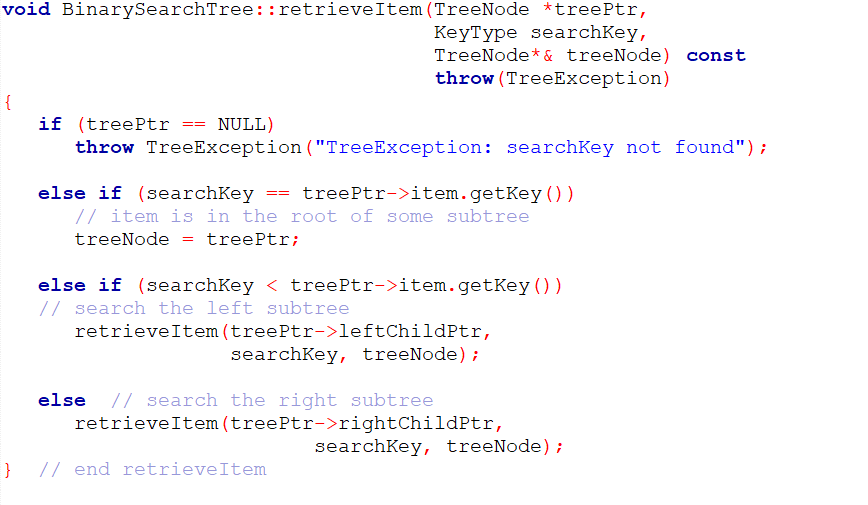


KeyedItem.h:
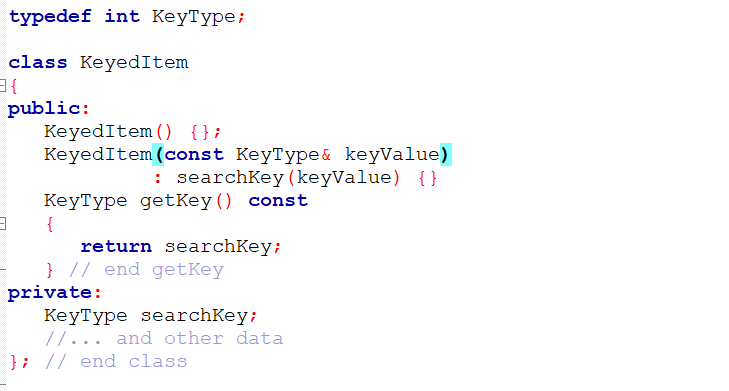
main.cpp:
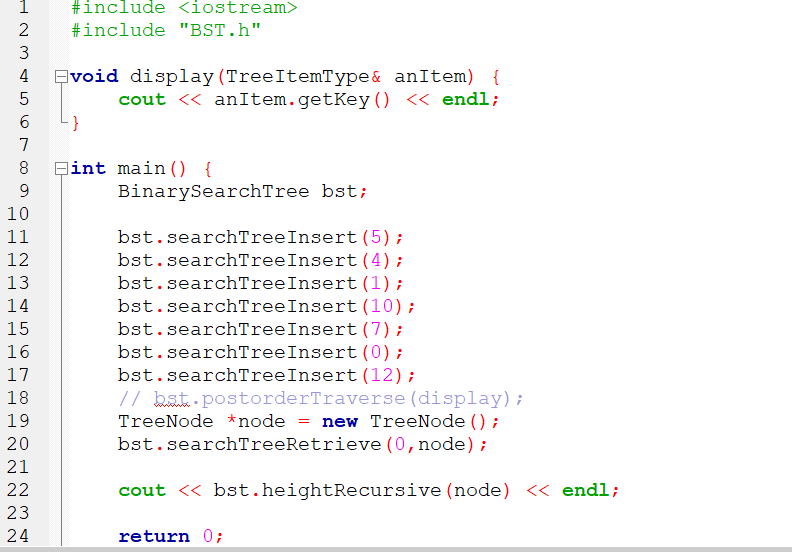
TreeNodeBST.h :
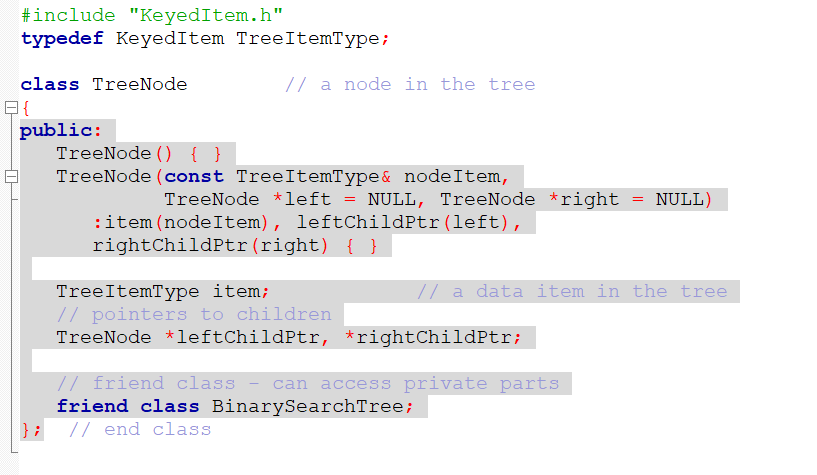
TreeException.h :
3) [65 points) For this part, use the implementation of BST.zip given on Blackboard. Write a new function AVLTreeInsert in the Binary Search Tree class, which performs an insertion as in an AVL tree, hence keeping the tree balanced. Write auxiliary functions when necessary. 4) (35 points] This part tests the code in the previous question. In the main function, insert 10,000 random integers using the usual insert of the Binary Search Tree class on one tree, and also using the AVLTreelnsert function on another tree. Compare the heights of the trees (You should anyway write a function computing the height of a tree). #include "BST.h" #include
7/ header file // definition of NULL BinarySearchTree::BinarySearchTree () : root (NULL) { -} // end default constructor BinarySearchTree::BinarySearchTree const BinarySearchTree& tree) { copyTree (tree root, root); -} // end copy constructor BinarySearchTree::-BinarySearchTree () { destroyTree (root); - } // end destructor int BinarySearchTree::height() const { return heightRecursive (root); void BinarySearchTree::searchTreeDelete (KeyType searchKey) throw (Tree Exception) 1 { deleteItem (root, searchKey); - } // end searchTree Delete void BinarySearchTree::searchTreeRetrieve (KeyType searchKey, TreeItemType & treeItem) const throw (TreeException) { // if retrieveItem throws a Tree Exception, it is // ignored here and passed on to the point in the code // where searchTreeRetrieve was called retrieveItem (root, searchkey, treeItem); } // end searchTreeRetrieve const void BinarySearchTree::searchTreeRetrieve (KeyType searchkey, TreeNode* & treeNode) throw (TreeException) { // if retrieveItem throws a TreeException, it is // ignored here and passed on to the point in the code // where searchTreeRetrieve was called retrieveItem (root, searchkey, treeNode); -} // end searchTreeRetrieve void BinarySearchTree::preorderTraverse (FunctionType visit) { preorder (root, visit); } // end pada Traverse void BinarySearchTree::inorderTraverse (FunctionType visit) { inorder (root, visit); } // end iman dan Traverse void BinarySearchTree: :postorderTraverse (FunctionType visit) { postorder (root, visit); } // end postorderTraverse void BinarySearchTree::insertItem (TreeNode *& treeptr, const TreeItemType& newItem) throw (TreeException) { if (treePtr NULL) { // position of insertion found; insert after leaf == // create a new node treePtr = new TreeNode (newItem, NULL, NULL); } // else search for the insertion position else if (newItem.getKey() item.getKey()) // search the left subtree insertItem(treePtr->left ChildPtr, newItem); else // search the right subtree insertItem(treePtr->rightChildPtr, newItem); // end insertItem void BinarySearchTree::deleteItem (TreeNode *& treePtr, KeyType searchkey) throw (Tree Exception) // Calls: deleteNodeItem. 1 { if (treePtr == NULL) throw Tree Exception ("Tree Exception: delete failed"); // empty tree else if (searchkey == treePtr->item.getKey()) // item is in the root of some subtree deleteNodeItem(treeptr); // delete the item // else search for the item else if (searchKey item.getKey()) // search the left subtree deleteItem(treePtr->leftChildPtr, searchKey); else // search the right subtree deleteItem(treePtr->rightChildPtr, searchKey); // end deleteItem -} void BinarySearchTree::deleteNodeItem (TreeNode *& nodePtr) // Algorithm note: There are four cases to consider: // 1. The root is a leaf. // 2. The root has no left child. 1/ 3. The root has no right child. 17 4. The root has two children. // Calls: processLeftmost. { TreeNode *delPtr; TreeItemType replacementItem; == = // test for a leaf if ( (nodePtr->leftChildPtr NULL) && (node Ptr->rightChildPtr NULL)) { delete node Ptr; node Ptr NULL; } // end if leaf // test for no left child else if (nodePtr->leftChildPtr NULL) { delPtr node Ptr; node Ptr = node Ptr->rightChildPtr; delPtr->rightChildPtr = NULL; delete delPtr; } // end if no left child == { == if (treePtr NULL) throw TreeException ("TreeException: searchKey not found"); == else if (searchKey treePtr->item.getKey()) // item is in the root of some subtree treeItem treePtr->item; else if (searchkey item.getKey()) // search the left subtree retrieveItem(treePtr->leftChildPtr, searchKey, treeItem); else // search the right subtree retrieveItem(treePtr->rightChildPtr, searchkey, treeItem); } // end retrieveItem void BinarySearchTree:: processLeftmost (TreeNode *& node Ptr, TreeItemType & treeItem) |{ if (node Ptr->leftChildPtr == NULL) { treeItem = node Ptr->item; TreeNode *delPtr = node Ptr; node Ptr = node Ptr->rightChildPtr; delPtr->rightChildPtr = NULL; // defense delete del Ptr; } else processLeftmost (node Ptr->leftChildPtr, treeItem); // end processLeftmost -} void BinarySearchTree:: retrieveItem (TreeNode *treeptr, KeyType searchkey, TreeItemType & treeItem) const throw (Tree Exception) { == if (treePtr NULL) throw TreeException ("TreeException: searchKey not found"); == else if (searchKey treePtr->item.getKey()) // item is in the root of some subtree treeItem treePtr->item; else if (searchkey item.getKey()) // search the left subtree retrieveItem(treePtr->leftChildPtr, searchKey, treeItem); else // search the right subtree retrieveItem(treePtr->rightChildPtr, searchkey, treeItem); } // end retrieveItem void BinarySearchTree:: retrieveItem (TreeNode *treePtr, KeyType searchkey, TreeNode* & treeNode) const throw (TreeException) { if (treePtr == NULL) throw Tree Exception ("TreeException: searchkey not found"); == else if (searchkey treePtr->item.getKey()) // item is in the root of some subtree treeNode treePtr; else if (searchKey item.getKey()) // search the left subtree retrieveItem(treePtr->leftChildPtr, searchKey, treeNode); else // search the right subtree retrieveItem(treePtr->rightChildPtr, searchkey, treeNode); } // end retrieveItem void BinarySearchTree::copyTree (TreeNode *treePtr, TreeNode *& newTreePtr) const // prendente traversal if (treePtr != NULL) { // copy node newTreePtr = new TreeNode (treePtr->item, NULL, NULL); copyTree (treePtr->leftChildPtr, newTreePtr->leftChildPtr); copyTree (treePtr->rightChildPtr, newTreePtr->rightChildPtr); } else newTreePtr NULL; // copy empty tree - } // end copyTree void BinarySearchTree::destroyTree (TreeNode *& treePtr) { // postorder traversal if (treePtr != NULL) { destroyTree (treePtr->leftChildPtr); destroyTree (treePtr->rightChildptr); delete treePtr; treePtr NULL; } // end if -} // end destroyTree void BinarySearchTree::preorder (TreeNode *treePtr, FunctionType visit) 1 { if (treePtr != NULL) { visit(treePtr->item); preorder (treePtr->leftChildPtr, visit); preorder (treePtr->rightChildPtr, visit); } // end if -} // end umeandaina void BinarySearchTree::inorder (TreeNode *treetr, FunctionType visit) { if (treePtr != NULL) { inorder (treePtr->leftChildPtr, visit); visit(treePtr->item); inorder (treePtr->rightChildPtr, visit); } // end if - } // end inander typedef int KeyType; class KeyedItem { public: KeyedItem() {}; KeyedItem (const KeyType & keyValue) : searchKey (keyValue) { } KeyType getKey() const . { return searchkey; } // end getKey private: KeyType searchkey; //... and other data }; // end class WNE #include #include "BST.h" Evoid display (TreeItemType & anItem) { cout #include using namespace std; class TreeException: public logic_error { public: TreeException (const string & message = "") : logic_error (message.c_str()) { } -}; // end TreeException























