1) You have been provided with a function, newSort, which sorts a list of integers provided as input and returns the sorted list. Analyze the correctness and efficiency of this function. Your analysis of the efficiency should include:

a) a clear and concise discussion of the running time and how it depends on the input,

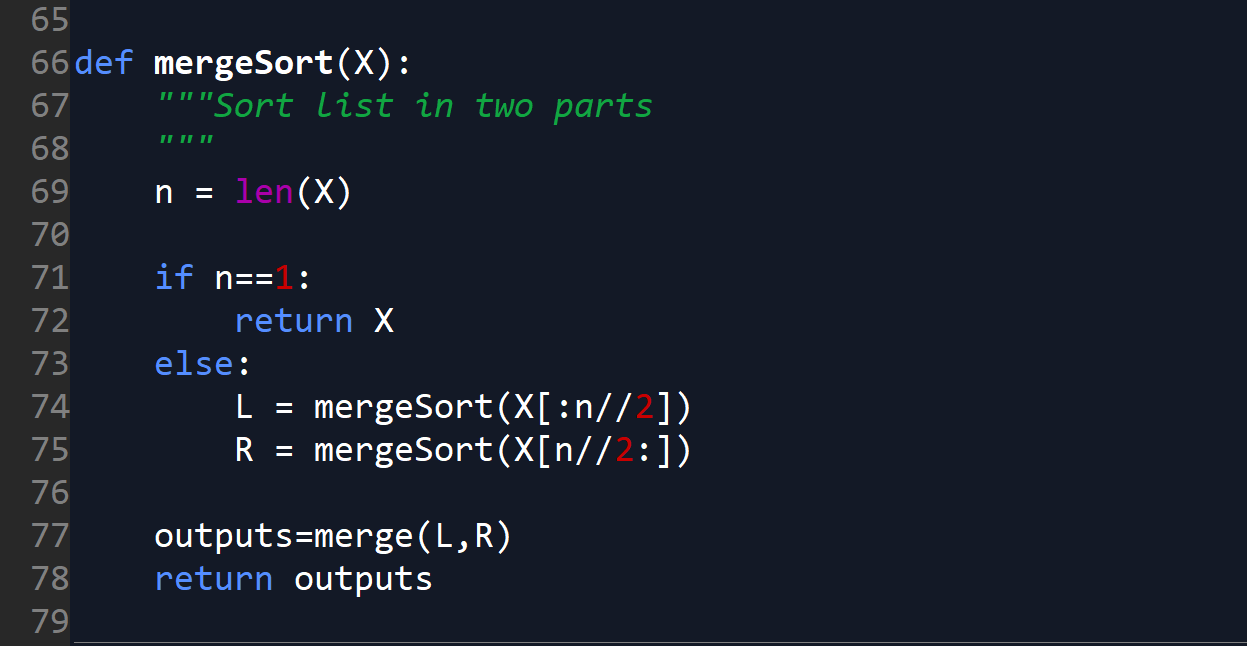
b) a critical comparison of newSort and merge sort, (analysis on running time, efficiency, cost and complexity)

**This page includes all information given for the task. One should explore the two sorting algorithms by initialiing different X and k. X is a list of unsorted random integers.**

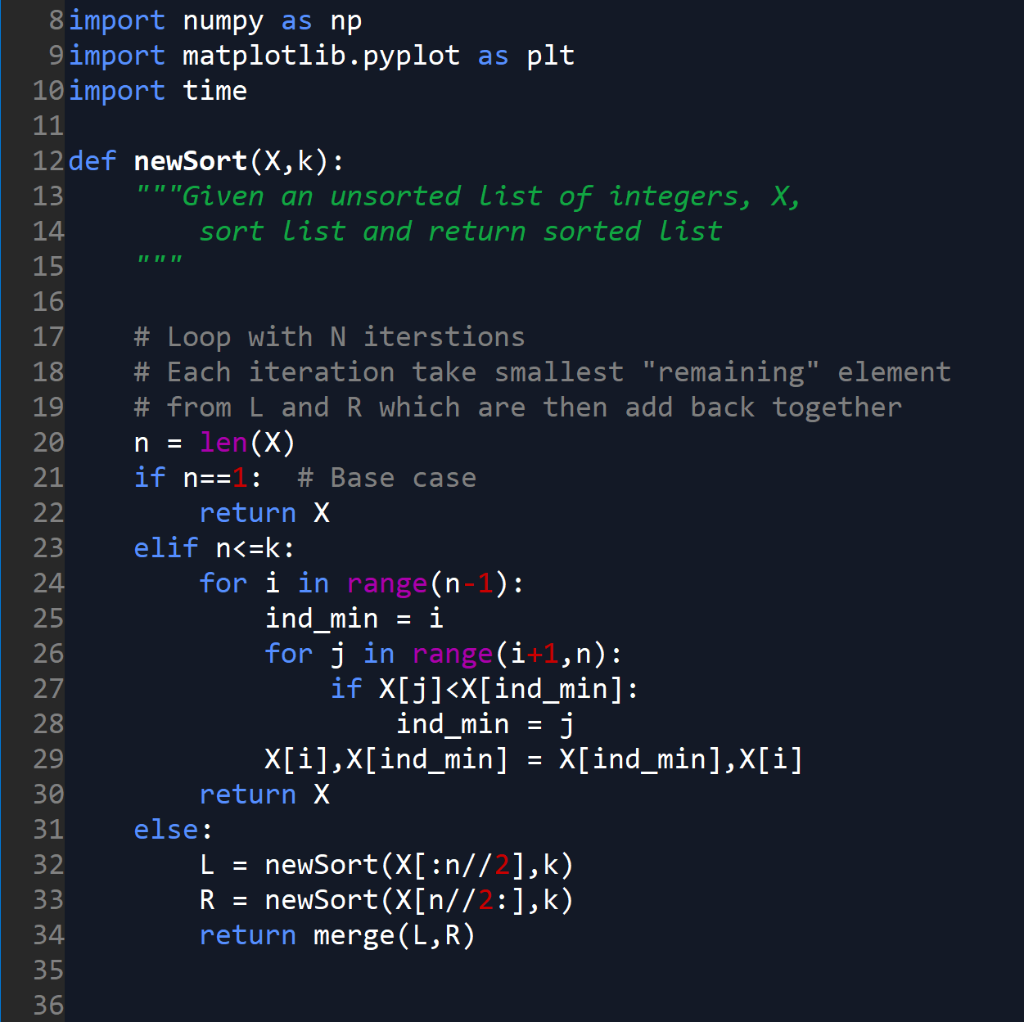
Here is the newSort that requires analysis:

import numpy as np import matplotlib.pyplot as plt import time

def newSort(X,k): """Given an unsorted list of integers, X, sort list and return sorted list """ # Loop with N iterstions # Each iteration take smallest "remaining" element # from L and R which are then add back together n = len(X) if n==1: # Base case return X elif n

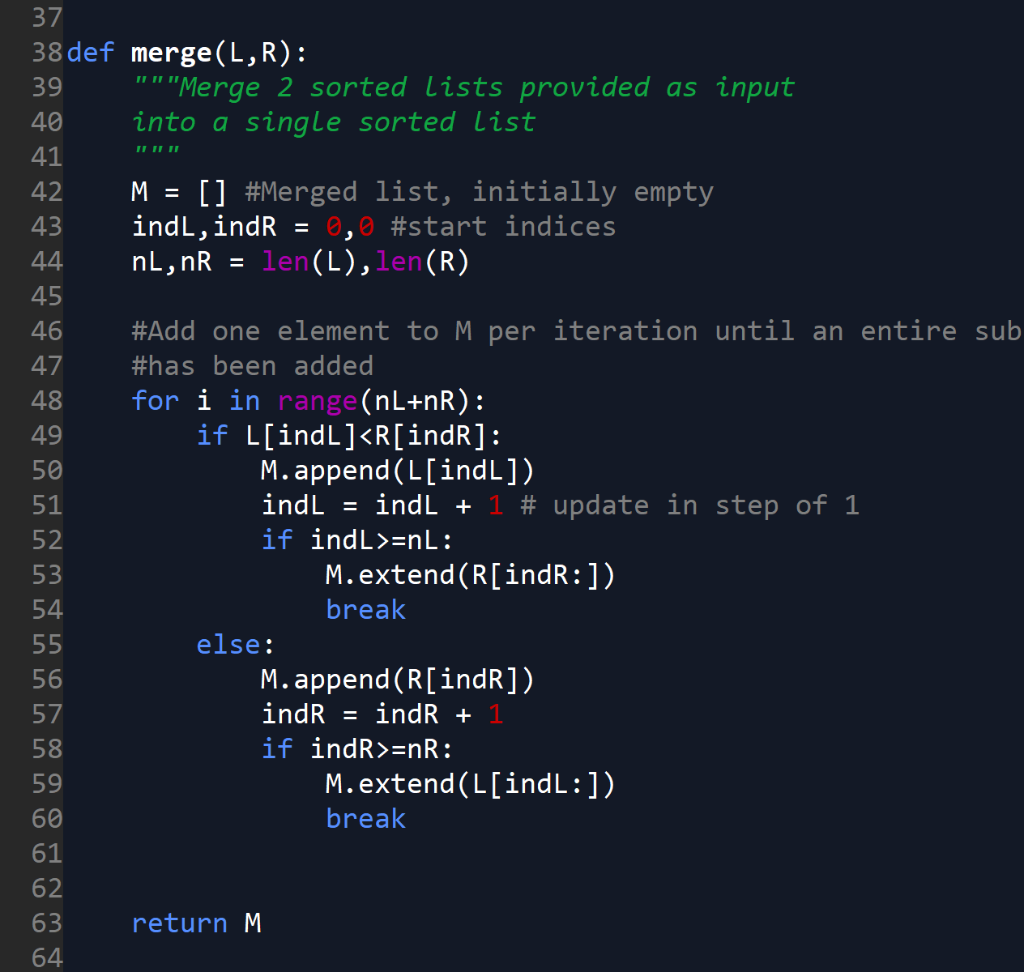
def merge(L,R): """Merge 2 sorted lists provided as input into a single sorted list """ M = [] #Merged list, initially empty indL,indR = 0,0 #start indices nL,nR = len(L),len(R)

#Add one element to M per iteration until an entire sublist #has been added for i in range(nL+nR): if L[indL]=nL: M.extend(R[indR:]) break else: M.append(R[indR]) indR = indR + 1 if indR>=nR: M.extend(L[indL:]) break return M

8 import numpy as np 9 import matplotlib.pyplot as plt 10 import time 11 12 def newSort(x,k): 13 """Given an unsorted list of integers, X, 14 sort list and return sorted list 15 21 22 23 24 25 # Loop with N iterstions # Each iteration take smallest "remaining" element # from L and R which are then add back together n = len(X) if n==1: # Base case return X elif n=nL: M.extend (R[indR:]), break else: M.append(R[indR]). indR = indR + 1 if indR>=nR: 'M.extend(L[indl:]). break 54 55 56 57 58 59 61 62 return M. 63 64. 65 66 def merge Sort(X): "Sort list in two parts 67 n = len(X) if n==1: return X else: L = mergeSort(X[:n//2]), R = mergeSort(x[n//2:]), outputs=merge(L, R) return outputs